| Взаимное расположение прямых в трехмерном пространстве – это область геометрии, изучающая взаимное положение прямых относительно друг друга. |
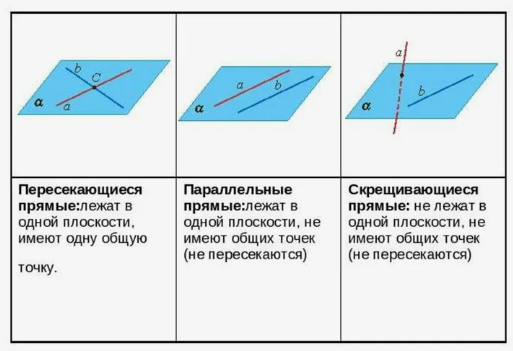
Прямые могут пересекаться в точке, образуя общую точку.
Прямые могут быть параллельными, не имея общих точек в трехмерном пространстве.
Две прямые считаются скрещивающимися, если они не лежат в одном плоскости, не являются параллельными или пересекающимися.
Две прямые считаются совпадающими, если все их точки совпадают.

1. Теорема о пересечении прямых в пространстве:
Если две прямые не параллельны, они пересекаются в точке, принадлежащей обеим прямым. Эта точка называется точкой пересечения прямых.
2. Теорема о параллельности прямых в пространстве:
Если две прямые имеют параллельные направляющие векторы (направляющие прямых), то эти прямые параллельны.
3. Теорема о совпадении прямых в пространстве:
Если две прямые совпадают, их уравнения одинаковы или пропорциональны.
4. Теорема о скрещивании прямых в пространстве:
Если одна из двух прямых лежит в плоскости, а вторая пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти прямые скрещиваются.
Взаимное расположение прямых в трехмерном пространстве имеет важное значение при решении задач из различных областей, таких как геометрия, физика, инженерия и компьютерная графика. Это позволяет определять, пересекаются ли прямые, параллельны ли они или совпадают ли их уравнения.
Тест по теме “Взаимное расположение прямых в пространстве”
Разбор:
Набранные баллы:
5
Смотреть разбор
Отправить тест на проверку?
Ты решил еще не все задания














