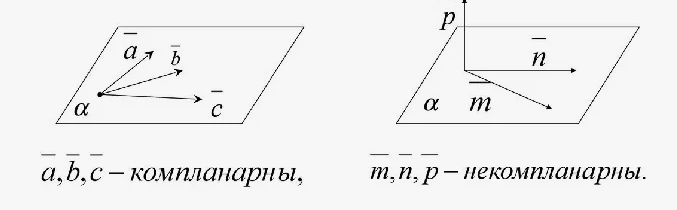Компланарность векторов – это свойство нескольких векторов  находиться в одной плоскости. находиться в одной плоскости. |
Это важное понятие в линейной алгебре и геометрии, широко применяемое в различных областях, включая физику, инженерные расчеты, компьютерную графику и многие другие.
Определение и признаки компланарности векторов:
Пусть имеется несколько векторов. Эти векторы называются компланарными, если они могут быть представлены в виде линейной комбинации их координат, соответствующих трехмерному пространству, а их концы лежат в одной плоскости.
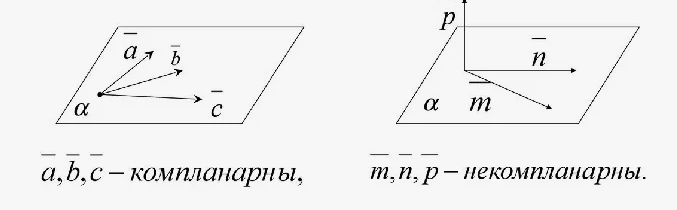

Признак компланарности трёх векторов
Если вектор  можно представить в виде
можно представить в виде  , где
, где  и
и  – некоторые числа, то векторы
– некоторые числа, то векторы  – компланарны.
– компланарны.
Основные признаки компланарности векторов:
- Если три вектора лежат в одной плоскости, они компланарны.
- Для четырех и более векторов существует определитель, который равен нулю, если они компланарны.
Порядок определения компланарности векторов
- Извлечение координат векторов:
Получение значений координат для каждого вектора  .
.
- Проверка линейной зависимости:
Проверка, может ли каждый вектор быть выражен в виде линейной комбинации других векторов.
Для четырех и более векторов вычисляется определитель из их координат, и если он равен нулю, то векторы компланарны.
Практическое применение компланарности векторов
В механике, электронике, аэродинамике компланарность векторов используется для определения равновесия системы сил, например, при анализе сил, действующих на твердое тело.
В трехмерной графике, дизайне и архитектуре компланарность векторов помогает при расстановке объектов в пространстве, создании моделей и визуализации различных конструкций.
В компьютерной графике и анимации компланарные векторы используются для определения ориентации и положения объектов в трехмерном пространстве.
Компланарность векторов – важное понятие в линейной алгебре и геометрии, имеющее широкое применение в различных областях. Знание этого концепта позволяет анализировать и определять положение векторов в трехмерном пространстве и применять его для решения задач в различных научных и технических дисциплинах.
Тест по теме “Компланарность векторов”
Разбор:
Набранные баллы:
5
Смотреть разбор
Отправить тест на проверку?
Ты решил еще не все задания