Единичная окружность является одним из ключевых понятий в математике и физике, она представляет собой окружность радиуса  с центром в начале координат на плоскости. Этот математический объект имеет значительное значение в различных областях науки и инженерии.
с центром в начале координат на плоскости. Этот математический объект имеет значительное значение в различных областях науки и инженерии.
Единичная окружность представляет собой геометрическую фигуру на плоскости с центром в точке ( , ,  ) и радиусом ) и радиусом  . . |
Её уравнение в декартовых координатах имеет вид  . Она является основой для понимания многих математических концепций, таких как тригонометрия, комплексные числа, и геометрия.
. Она является основой для понимания многих математических концепций, таких как тригонометрия, комплексные числа, и геометрия.
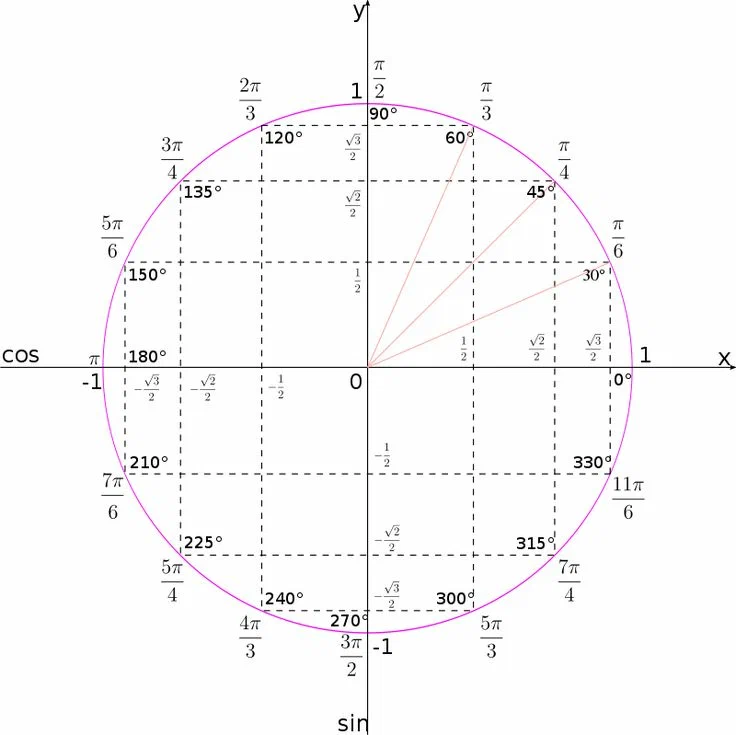

Единичная окружность является основой для изучения тригонометрических функций. Она позволяет установить связь между углами и значениями синуса и косинуса. Так, значения синуса и косинуса угла можно представить как координаты точки на окружности.
Единичная окружность играет важную роль в теории комплексных чисел. Каждое комплексное число может быть представлено как точка на плоскости, и если модуль этого числа равен  , то оно лежит на единичной окружности.
, то оно лежит на единичной окружности.
В физике единичная окружность применяется для описания периодических процессов, например, колебаний и волн. Фазовые диаграммы и векторные диаграммы используют этот инструмент для визуализации и анализа таких процессов.
- Тригонометрические функции:
Используйте окружность для визуализации значений тригонометрических функций (синус, косинус, тангенс и т.д.). Углы могут быть измерены от начальной точки  , что упрощает вычисления.
, что упрощает вычисления.
- Графическое представление комплексных чисел:
Для представления комплексных чисел в виде точек на плоскости используйте единичную окружность. Модуль комплексного числа, равный  , поможет увидеть его на этой окружности.
, поможет увидеть его на этой окружности.
- Анализ фазовых процессов:
Для изучения фазовых изменений в физических или инженерных системах используйте векторные диаграммы на единичной окружности.
Единичная окружность представляет собой важный математический инструмент, широко используемый в различных областях науки и инженерии. Она служит основой для понимания тригонометрии, комплексных чисел, физических процессов и имеет большое значение для графического представления и анализа различных явлений. Ознакомление с этим концептом поможет лучше понять и применять математические и физические принципы в различных областях знаний.
| Прямоугольная система координат – это метод для описания точек на плоскости или в пространстве. |
Он использует две взаимно перпендикулярные оси – горизонтальную ось  и вертикальную ось
и вертикальную ось  . Точка в этой системе задается уникальной парой чисел
. Точка в этой системе задается уникальной парой чисел  , где
, где  – это расстояние по горизонтальной оси, а –
– это расстояние по горизонтальной оси, а –  по вертикальной оси от начала координат.
по вертикальной оси от начала координат.
| Радиус – это расстояние от центра окружности (или сферы) до любой точки на её границе. |
Для единичной окружности радиус равен  . В уравнении единичной окружности
. В уравнении единичной окружности  радиус определяет длину от центра до любой точки на окружности.
радиус определяет длину от центра до любой точки на окружности.
| Радиан – это единица измерения угла, основанная на радиусе единичной окружности. |
Один радиан соответствует углу, образованному двумя лучами, их начала в центре окружности и концов, лежащих на окружности, когда длина дуги между ними равна длине радиуса. Число  радиан соответствует полному обороту по окружности.
радиан соответствует полному обороту по окружности.
Длина окружности вычисляется как произведение радиуса на  . Для единичной окружности, где радиус равен
. Для единичной окружности, где радиус равен  , длина окружности будет
, длина окружности будет  единиц.
единиц.
Эти понятия имеют важное значение в геометрии, тригонометрии и физике. Они помогают описывать и изучать геометрические формы, измерять углы и длины окружностей, что является фундаментальным для решения множества математических и физических задач.
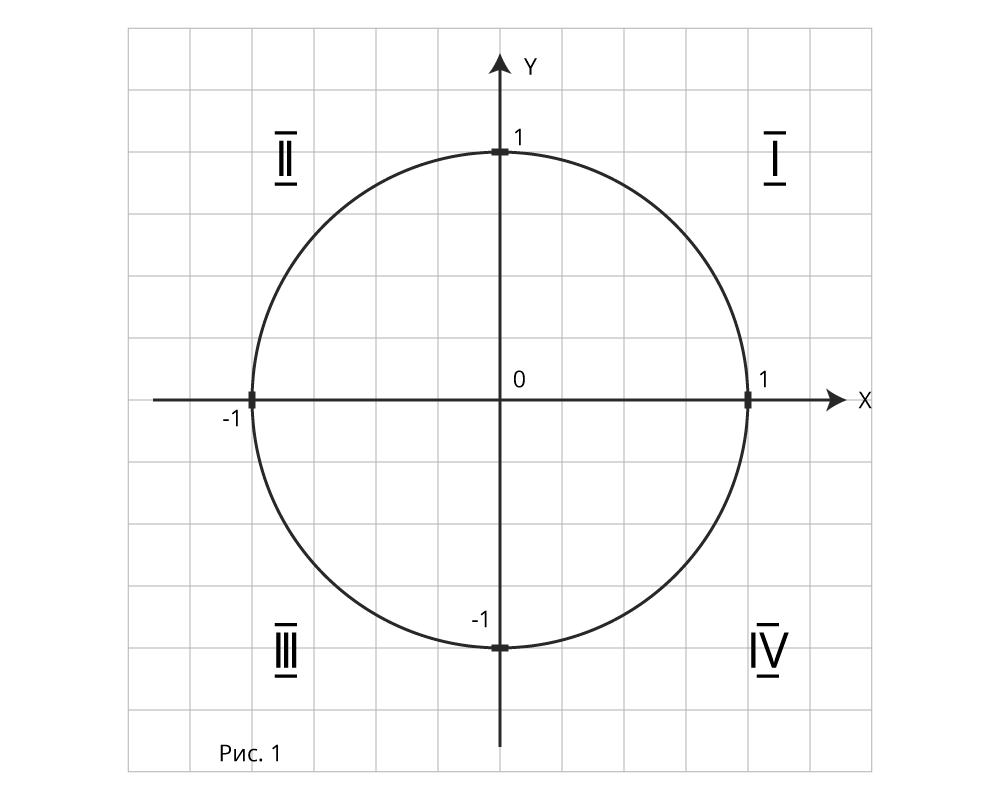
Единичная окружность разделена на  четверти:
четверти:
 – положительный косинус и синус;
– положительный косинус и синус;
 – отрицательный косинус и положительный синус;
– отрицательный косинус и положительный синус;
 – отрицательный косинус и синус;
– отрицательный косинус и синус;
 – отрицательный синус и положительный косинус.
– отрицательный синус и положительный косинус.
Тест по теме “Единичная окружность”
Разбор:
Набранные баллы:
5
Смотреть разбор
Отправить тест на проверку?
Ты решил еще не все задания
с центром в начале координат на плоскости. Этот математический объект имеет значительное значение в различных областях науки и инженерии.
. Она является основой для понимания многих математических концепций, таких как тригонометрия, комплексные числа, и геометрия.












