Законы алгебры логики

Алгебра логики позволяет определить истинность или ложность высказывания, не вникая в его содержание. Следовательно, любое высказывание может принимать только два значения — истину(1) или ложь(0). В этой статье мы разберемся с этим термином подробнее и дадим тебе теоретическую информацию, которая пригодится тебе на экзамене!

В алгебре логики существуют 3 основные операции, выполняемые над высказываниями:

1. Конъюнкция (логическое «и», которое обозначается символом & или ‘/\’)

2. Дизъюнкция (логическое «или», обозначается символом | или \/)

3. Отрицание (обозначается знаками ! или чертой над буквой)

Приведем пару примеров логических операций:

В естественном языке конъюнкция обычно передается союзами «и», «а», «но» и конструкциями типа «в то же время», «одновременно», «вместе» и так далее. Примеры конъюнкции можно увидеть в высказываниях «Пошел дождь, и я спрятался под навес».

Примером дизъюнктивного высказывания может быть суждение «Идет дождь, или идет снег».

Отрицание используется с предлогом НЕ: 

Сегодня я НЕ пошел в школу

Это был НЕ лучший день

Деньги взял НЕ брат, а сестра

Как и в любом разделе математики, в алгебре логики существуют свои законы и правила, определяющие логику работы всего данного раздела. Рассмотрим их:

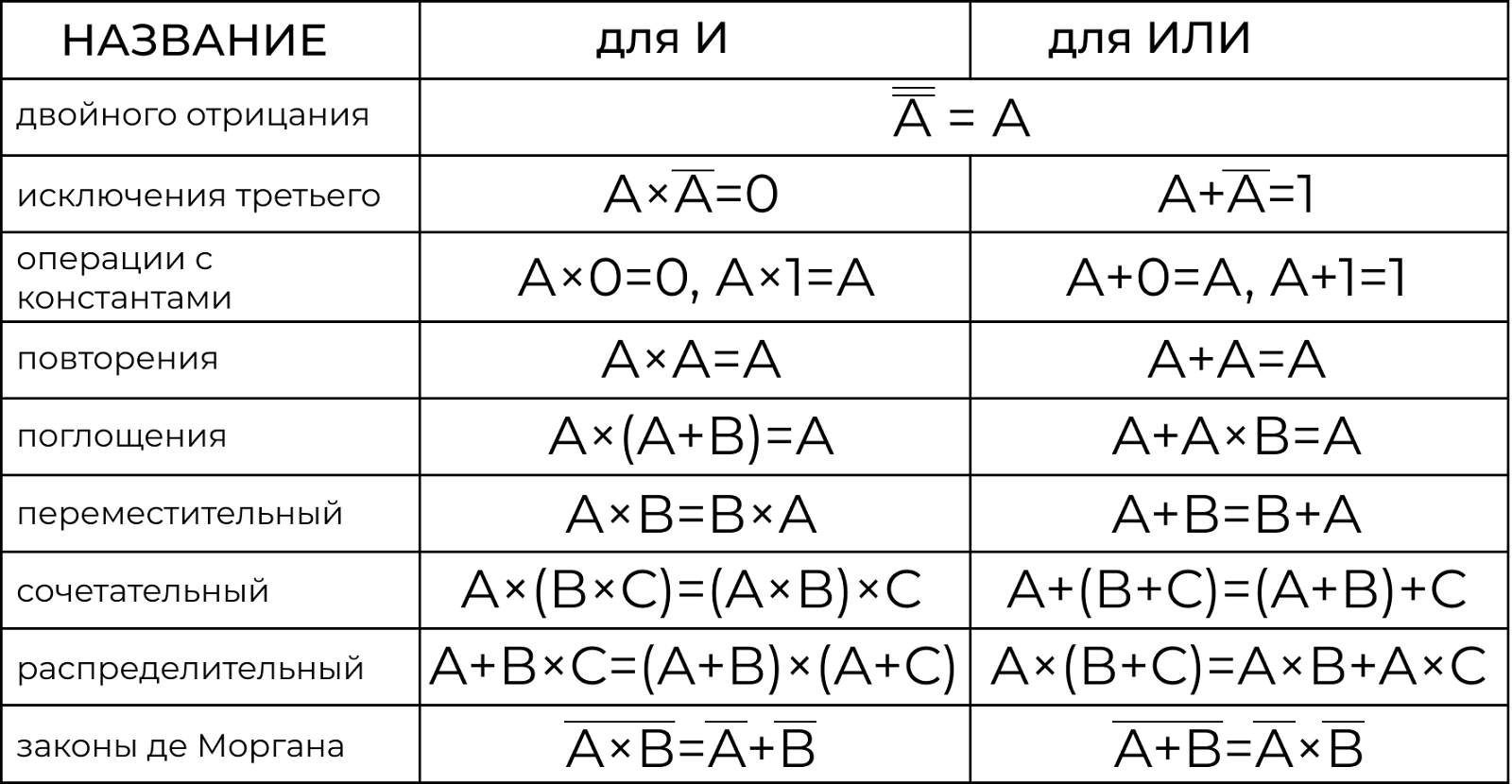
Закон двойного отрицания работает по одному простому правилу — если мы отрицаем отрицание, значит мы говорим истину. Для примера подойдет фраза «Я не не сделал домашнее задание» -> «Я сделал домашнее задание»

Закон исключения третьего и операции с константами подчиняются правилам обыкновенной математики — при умножении на ноль всегда будет ноль, а при умножении на 1 получается то же самое число. 

Закон повторения: Если вспомнить, что в логике существует только два значения (0 и 1), то 0 * 0 и 1 * 1 правильно будет просто сократить

Закон поглощения доказывается с помощью таблицы истинности, по которой будет видно, что переменная поглощает оставшееся выражение, если все выражение имеет данный вид

Переместительный закон прост — от перестановки слагаемых или множителей сумма, как и произведение, не меняется

Сочетательный закон — применяется, когда есть или только операция дизъюнкции, или только операция конъюнкции. Тогда можно обходиться без скобок или хаотично ставить скобки.

Распределительный закон работает точно так же, как и обыкновенное раскрытие скобок в школьной математике, однако, если для дизъюнкции это и так понятно, то для конъюнкции данный закон еще придется доказать

Закон двойственности и инверсии (закон Моргана) — основоположником данного правила стал шотландский математик и логик де Морган. Он разработал правило, которое связывает конъюнкцию и дизъюнкцию с помощью отрицания.