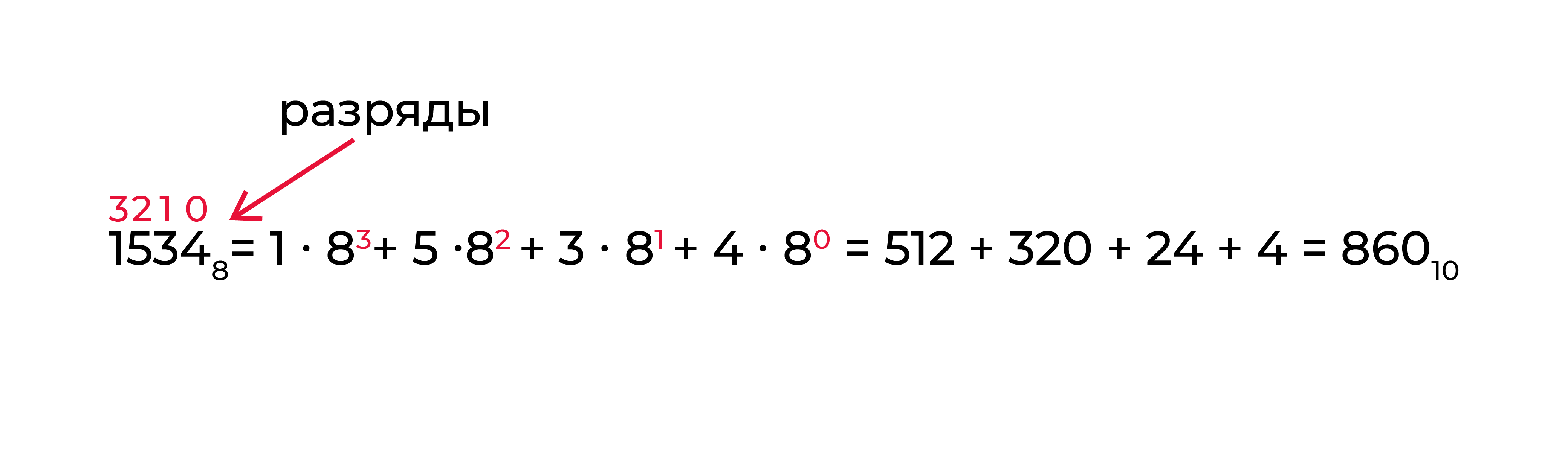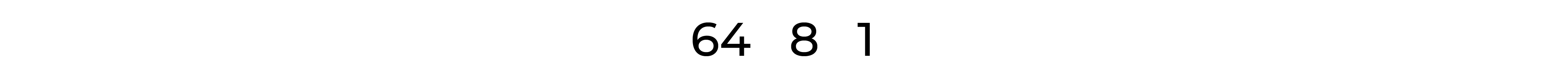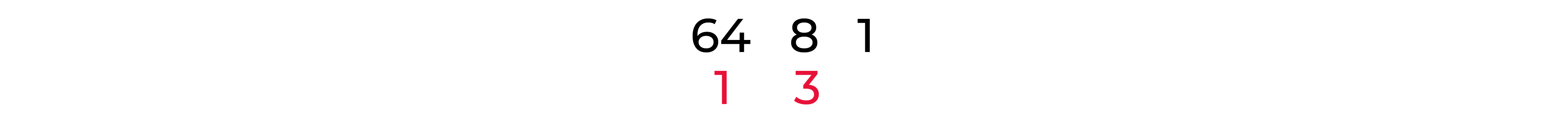Ускоренный способ перевода

Продолжая изучать системы счисления, нужно поделиться с вами и разными способами перевода чисел в другие системы счисления, так как это основополагающая задача во многих номерах ЕГЭ.

Есть два метода перевода:

1.  Из 10 СС в любую другую
2. Из любой другой в 10 СС

Давайте начнем с первого. Допустим, у нас есть десятичное число, как же нам его представить в 2-ичном виде? В школе тебе наверняка рассказывали про метод деления. 

Суть проста: для того, чтобы перевести число из 10-СС в любую другую, тебе необходимо последовательно делить число на основание этой системы счисления, пока это возможно. Остатки от деления, записанные в обратном порядке, и будут образовывать число в этой системе счисления.

• Давай рассмотрим на примере перевод числа 4510 в 2-ичную систему:
  
  

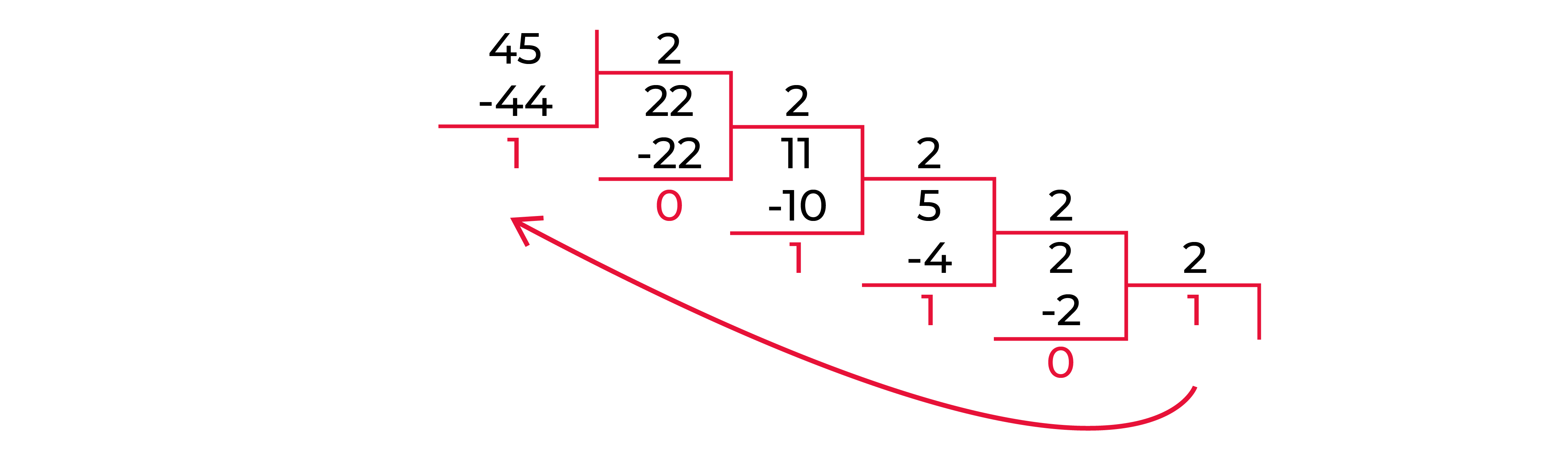
• 45/2 = 22, остаток: 1
  22/2 = 11, остаток: 0
  11/2 = 5, остаток: 1
  5/2 = 2, остаток: 1
  2/2 = 1, остаток: 0
  1/2 = 0, остаток: 1
  4510 = 1011012

Или, например, перевод числа 12610 в 16-ичную систему:

• 
  126/16 = 7, остаток: 14, 14 = E
• 7/16 = 0, остаток: 7

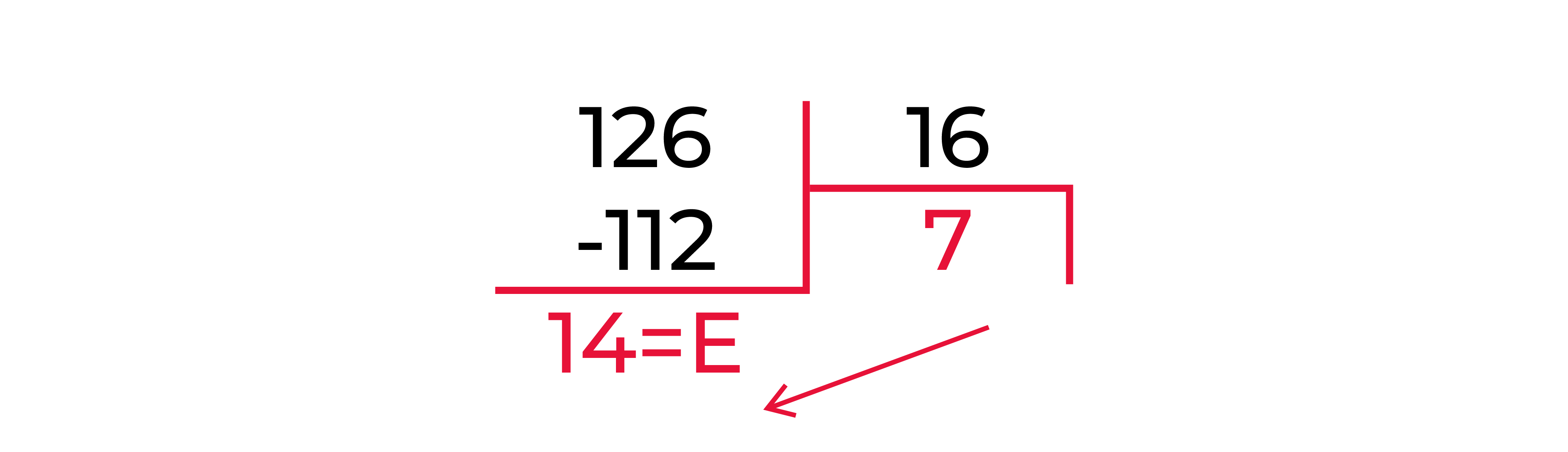
12610 = 7E16

Примечание: неважно основание какой системы счисления больше! Перевод 10-ичного числа и в 2-ичную, и в 7-инчую, и в 16-ичную систему производится по одному и тому же правилу.

Здесь все понятно, схема довольно простая, но как же теперь перевести число из какой-нибудь системы счисления в привычную нам десятичную? Этот алгоритм тоже довольно легок и основывается на разложении числа. Если взять десятичное число 3510, то его без проблем можно представить в виде:

Возьмем число и представим его таким же способом:

Вау, все сошлось, а значит схема действительно работает, и ее можно использовать для перевода, давайте сформулируем правило:

Для перевода числа из любой системы счисления в 10-ичную необходимо проставить разряды в числе справа налево с нуля в порядке возрастания, а затем умножать цифру на основание системы счисления в степени этого разряда. Ответ: сумма всех множителей. 

Пример:

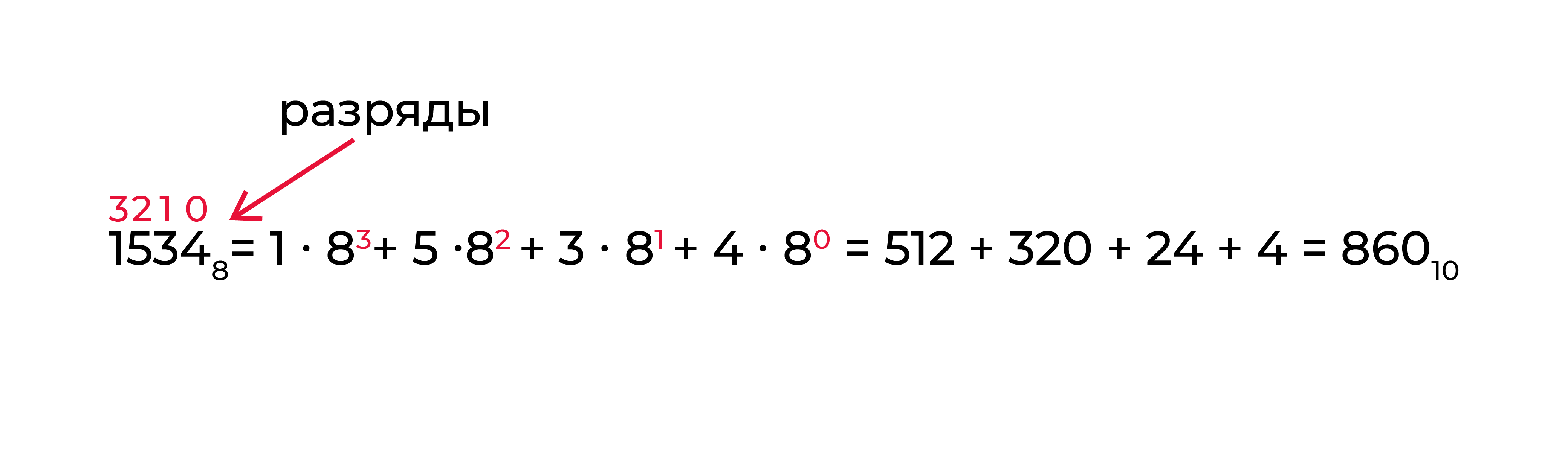
Давайте попрактикуемся и переведем несколько чисел:

Кстати, зная это свойство можно оптимизировать способ перевода из десятичной системы счисления. Иногда делить приходится очень долго, так давайте просто собирать наше число из степеней его основания.

Например: 

• 5 можно представить как 4+1, а это 22 + 20 = 1012  
  8 можно представить как 23 = 10002

 
Давай переведем число 19510 в 2-ичную систему использую этот способ:

• Выпишем все степени двойки не превышающие 195 в порядке убывания:

128   64   32   16   8   4   2   1

• Далее считаем сколько раз 128 входит в исходное число 195, очевидно всего лишь 1 раз, поэтому под 128 мы ставим единицу, а из числа 195 вычитаем 128 и получаем, что нам остается собрать еще 67

• Продолжаем эту операции пока не укомплектуем итоговое число:
   

Сколько раз 64 входит в 67? Всего 1, ставим под 64 единицу, и вычитаем 67-64=3 значит нам остается собрать всего лишь 3.

• Ни 32, ни 16, ни 8, ни 4 не входят в 3, потому что они больше ее, значит на их местах ставим 0, а вот 2 в 3 входит, поэтому там ставим 1, и нам остается собрать всего лишь 3-2=1

• 1 входит в 1 ровно 1 раз, ставим там 1 и на этом наш перевод закончен
   

Получили число 110000112:

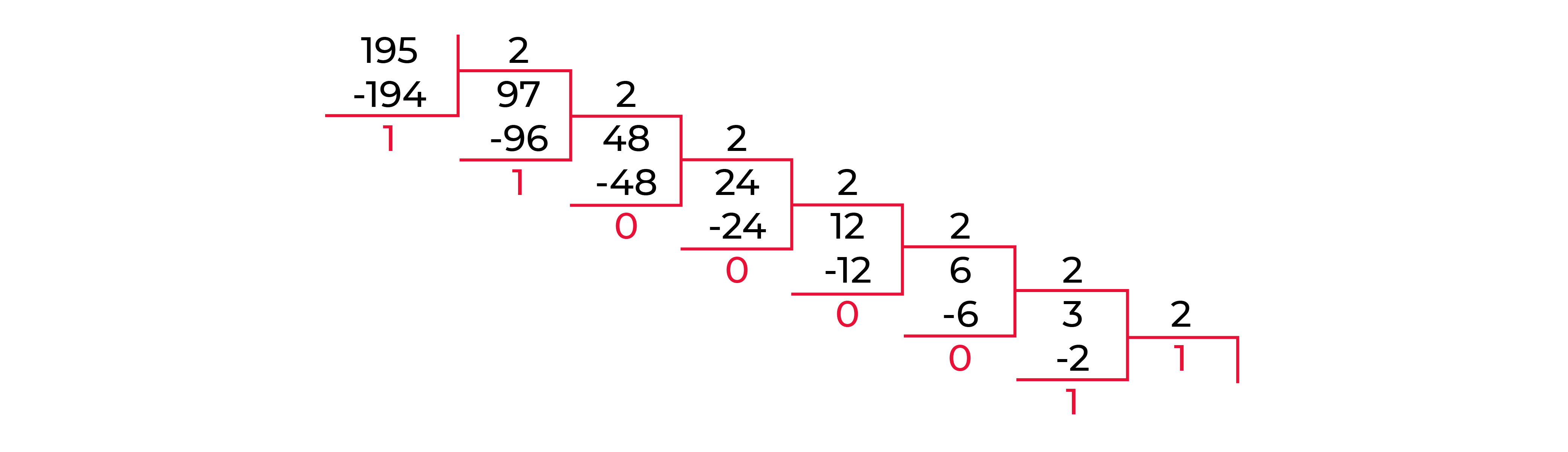
• 195/2 = 97, остаток: 1
• 97/2 = 48, остаток: 1
• 48/2 = 24, остаток: 0
• 24/2 = 12, остаток: 0
• 12/2 = 6, остаток: 0
• 6/2 = 3, остаток: 0
• 3/2 = 1, остаток: 1
• 1/2 = 0, остаток: 1
• 19510 = 110000112
   

Довольно громоздко, согласись? 

В заключение давай переведем еще число 90 в 8-ичную систему:

• Выписываю степени 8, не превышающие 90, в порядке убывания

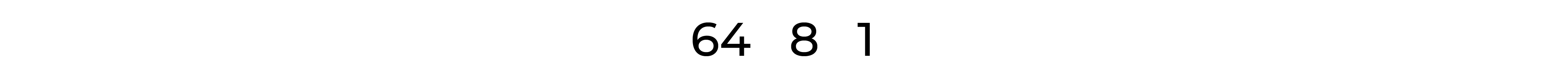
• 64 входит в 90 один раз, ставлю единицу, еще собрать осталось 90-64 = 263) 8 входит в 26 три раза, ставлю тройку, еще собрать осталось 26-3*8 = 2

• 8 входит в 26 три раза, ставлю тройку, еще собрать осталось 26-3*8 = 2

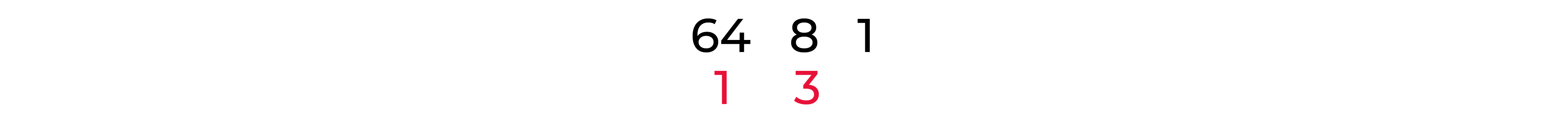
• 1 входит в 2 два раза, ставлю 2, конец. 

Надеюсь, теперь вы понимаете, как устроены системы счисления и сможете без проблем с ними работать, особенно с помощью ускоренного способа, ведь это намного быстрее.