В прошлой статье мы рассмотрели системы счисления и разницу между ними. А в этой разберем прямой способ перевода между системами. Несомненно, зная два основных способа перевода, можно перевести любое число в любую систему счисления, сначала переведя ее в десятичную, а затем уже в любую другую. 

Однако данный метод слишком долгий и не всегда удобный. Раскрою тебе тайну: существует способ прямого перевода между основаниями, которые являются степень одного и того же числа, например, можно быстро перевести число из 8-ричной в 16-ричную или из 3-ичной в 9-ичную.

Для того, чтобы осуществить перевод между основаниями, являющимися степенью двойки, необходимо, разбить число на группы (пары, триады, тетрады…), равными степени двойки этого числа. Например, число 8 является 3-ей степенью двойки, поэтому я бы разбивал число на триады (группы по три цифры).

Далее каждую группу отдельно перевести в двоичную систему, и всё число снова разбить на группы, которые равны степени двойки конечной системы, в которую осуществляется перевод. Перевести каждую группу в нужную СС, и готово. 

Согласен, на первый взгляд звучит страшно и непрактично, но давайте рассмотрим на примере: 

Для удобства пока что будем пользоваться таблицей, в которой все числа уже переведены заранее:

Давайте попробуем перевести число  из 8-ичной системы в 16-ричную. Моя система 8-ричная –  это , значит каждое число я буду заменять на триады (группы по 3). 

Там, где это необходимо, дополняю число незначащими нулями, как, например, в случае с тройкой,  это , но раз мы пишем триады, то ставлю перед этим незначащий ноль. Получили число 001101011110₂ первые два незначащих нуля можно убрать,  и результат 1101011110₂ нужно перевести в 16-ринчую систему,  , значит нужно разбить мое число на тетрады (группы по 4). Затем каждую тетраду перевести в 16-ричную систему и получить ответ.

Примечание: важно выполнять действие справа налево, чтобы при необходимости дополнить число слева незначащими нулями!

Получаем ответ 35E₁₆. Давайте выполним проверку и убедимся, что мы все сделали верно:

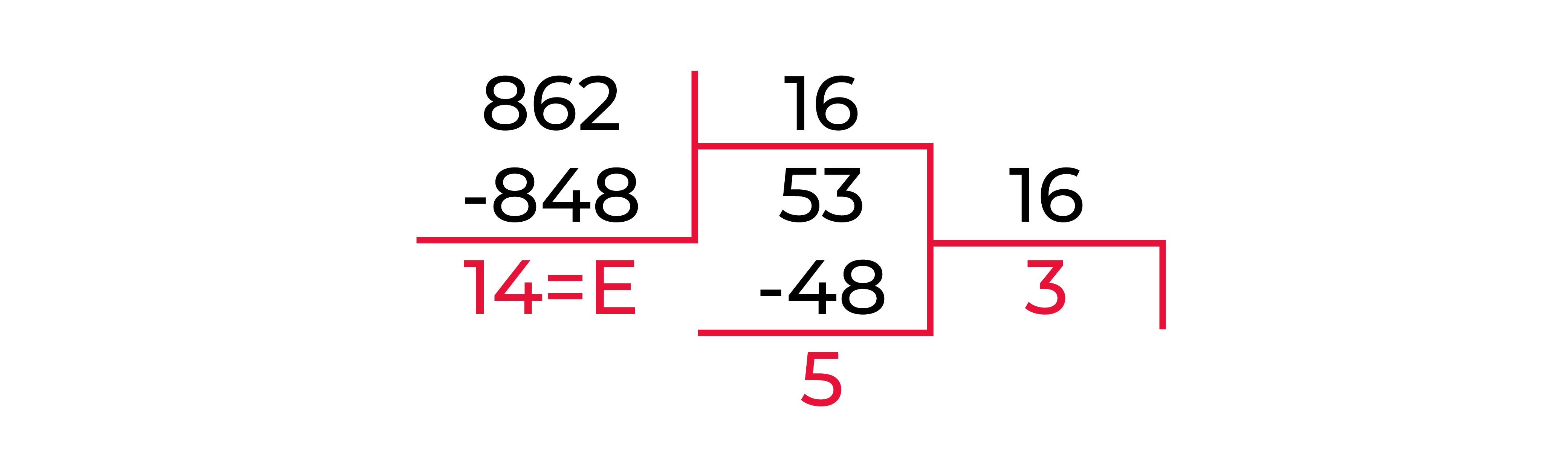
Все действительно так и есть.

Теперь попробуем перевести число 18A₁₆ в 4-ричную систему:

Делаю все тоже самое: сначала каждую цифру числа 18A₁₆ заменяю на 4 цифры двоичной системы (тетрады), затем это число слева направо делю на группы по 2 цифры, так как мне нужна 4-ричная система, а в конце перевожу каждую цифру. 

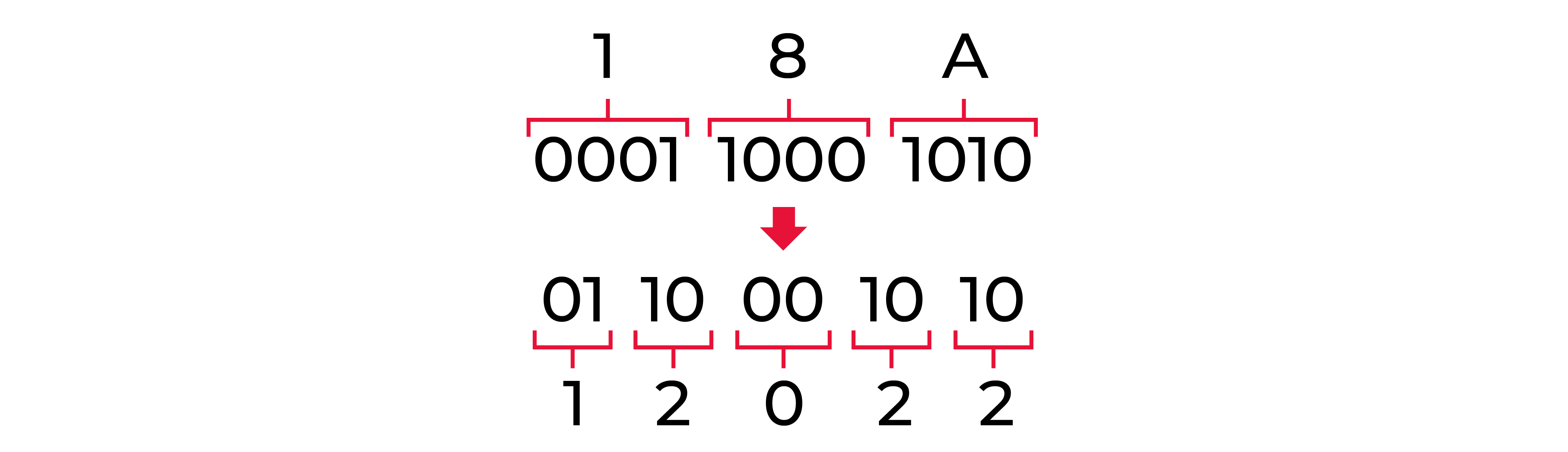
В результате получаем число 12022₄ 

Проверка:

18A₁₆ 

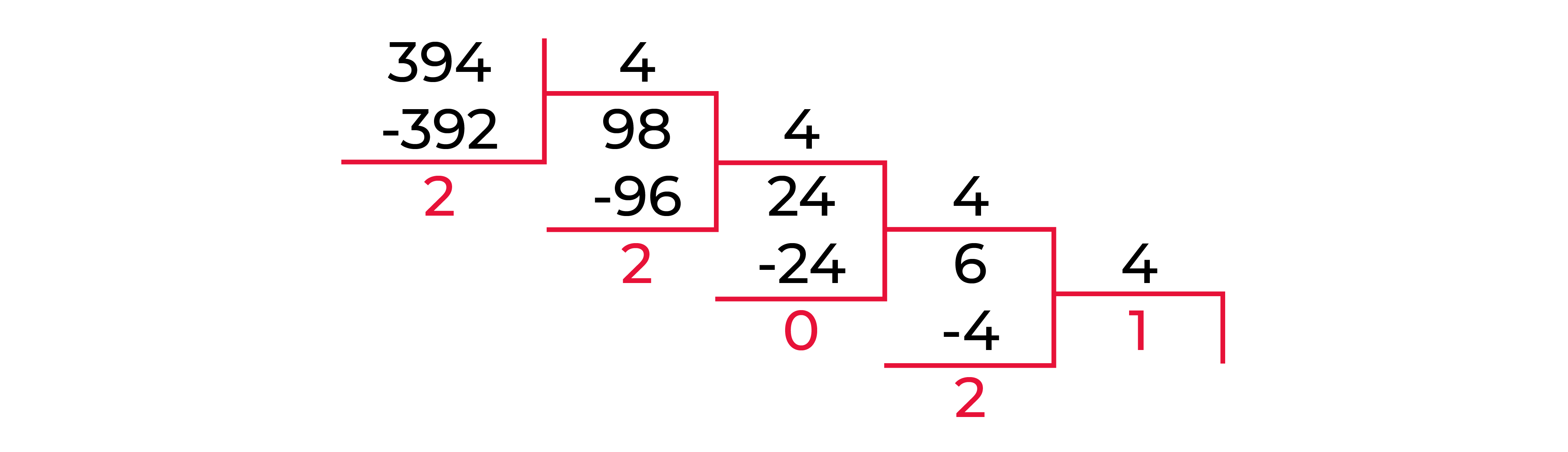
Все верно.

Наше правило позволяет сделать прямой перевод между степенями любых чисел.

Попробуем перевести число  в 9-ричную систему счисления:

Все по стандарту: мое число уже находится в троичной системе, поэтому его никуда переводить не нужно, достаточно просто разбить его на группы по 2 цифры,  так как . А каждую группу отдельно перевести в 9-ричную систему:

1₃ = 1₉
20₃ = 6₉

Ответ: 

Проверка:

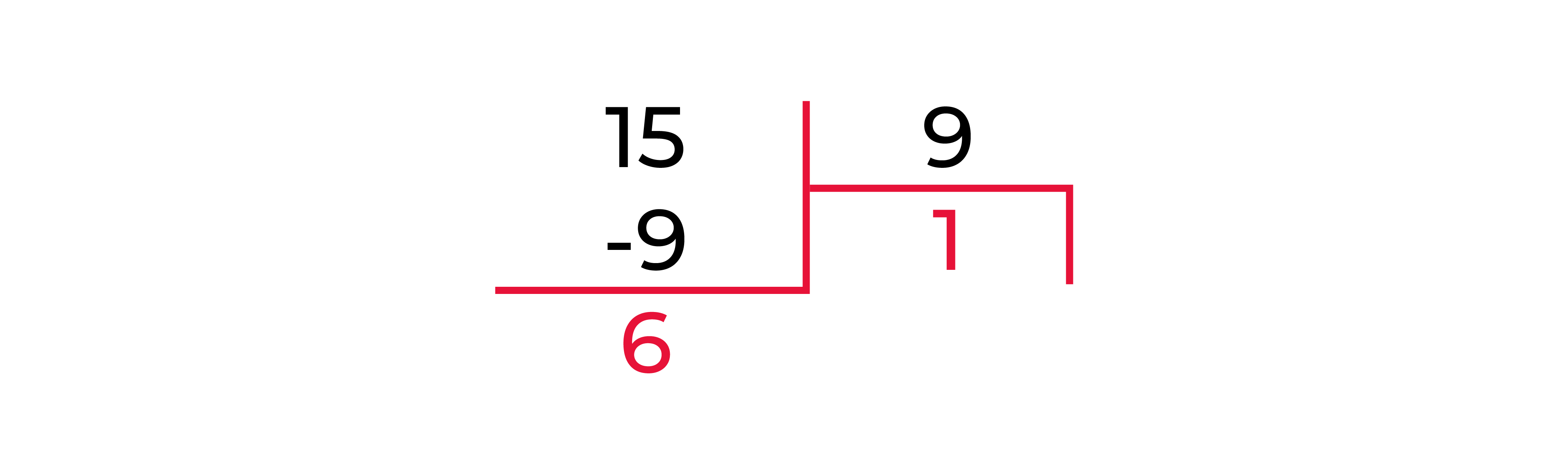
Ответ, без сомнений, равен .

Эти знания сильно помогут в понимании работ систем счисления, что в свою очередь, сильно пригодится в кодировании и комбинаторике.