В этой статье мы рассмотрим сочетания и задания по этой теме, которые могут встретиться на экзамене. Если эта тема тебе непонятна, обязательно читай статью.
| Сочетание – количество всевозможных комбинаций k элементов из набора n элементов. |
Но главным отличием от размещения является неупорядоченность комбинаций. Если для размещения комбинации (a, b)≠(b, a) не равны, то для сочетаний a, b=(b, a) – одна и та же комбинация. Сочетания используются тогда, когда порядок не важен!

Рассмотрим пример
- Из трех учеников нужно выбрать двух дежурных. Сколькими способами это можно сделать?
- В нашем примере нам необходимо выбрать из набора n=3 элементов, k=2 элемента, в данном случае – учеников. Здесь порядок отбора не важен, так как две должности дежурного одинаковые. Каждый кандидат может войти только один раз в выборку. Распишем варианты выборки:
первый ученик + второй ученик
первый ученик + третий ученик
второй ученик + третий ученик
- Возникает вопрос: почему мы не можем взять ещё и второй ученик + первый ученик? Ответ очевиден, у нас порядок не важен, (первый ученик + второй ученик) = (второй ученик + первый ученик) – это одна и та же комбинация. Почему? Представь ситуацию: тебя и Петю выбрали дежурными, разве Петя и ты это будет другая комбинация? Нет, это всё та же комбинация.
- Теперь посмотрим на эту задачку со стороны правила произведения: На первое место можем поставить всех 3х учеников, тогда на второе – уже двух, так как одного уже выбрали, получаем:
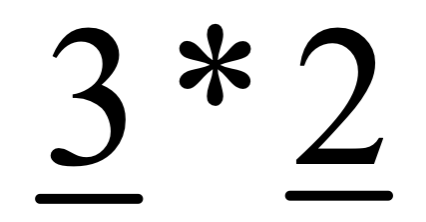
- Похоже на формулу размещений без повторений… Да, это так, получается, мы не учли, что (первый ученик + второй ученик) = (второй ученик + первый ученик) – это одна и та же комбинация и т.д. Тогда нужно разделить на 2!. Почему именно на факториал? Так у нас может быть выборка из большего числа элементов. А как мы с вами знаем, k предметов можно переставить k! различными способами, поэтому будем делить на k!.
- Таким образом получаем ответ 3*2/2! = 3 комбинации.
Теперь дадим определение
| Сочетаниями без повторений из n различный элементов по k элементов называются всевозможные комбинации k различных элементов, выбранных из исходных n, в которых порядок не важен, без повторений. |
Их число вычисляется по выведенной формуле:

Вроде, понятно, супер, идём дальше!
Рассмотрим эту же задачку на графах
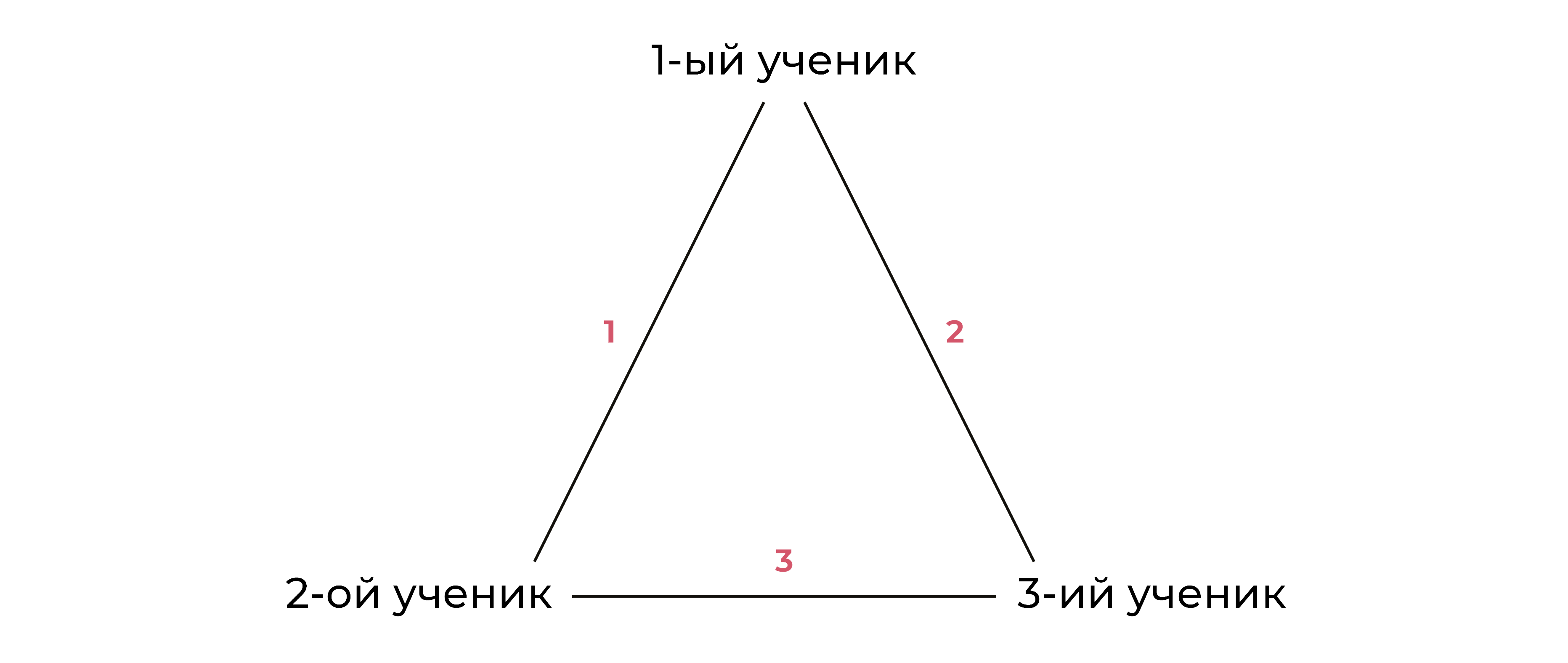
- Мы построили граф из трех учеников, можно посчитать количество ребер в графе – оно равно 3, также как и наш ответ на это же задание. Почему так? Граф не соединяет два раза 2 одинаковых пункта, также один пункт с собой тоже не соединяет, таким образом, исключая все неподходящие варианты для сочетаний.
- Теперь можно рассмотреть одно свойство сочетаний. Как думаешь
 ? Давай проверим. Вычислим два значения по формуле:
? Давай проверим. Вычислим два значения по формуле:


Оказывается, действительно,  равны! Удивительно, правда?
равны! Удивительно, правда?
На самом деле, ничего удивительного, мы же из n вычитаем k и делим на факториал полученного значения и факториал k. Так и получается, что сумма k и (n-k) равна n, а значит противоположные значения равны. А если простым языком, то количество способов выбрать k из n элементов равно количеству способов не выбрать (n-k) элементов из n.
Задача: В некотором классе 4 ответственных ученика. Сколькими способами можно выбрать трех дежурных?
Решение: Так как должностей дежурного 3, значит, порядок не важен, можно воспользоваться формулой сочетаний без повторений. В нашем случае надо выбрать 3 дежурного из четырех учеников:

Наш граф выглядел бы так:

Всего получилось 4 таких треугольника.Таким образом, мы получили ответ 4.
Теперь рассмотрим сочетания с повторениями
Попробуем вывести формулу с помощью примера:
Пусть в кондитерском магазине продаются пирожные четырех видов: эклеры, песочные, картошка, корзиночки. Будем разделять виды пирожных палочками |. Если куплено 3 корзиночки, 1 картошка, 2 песочных, 1 эклер, то получим такую запись: 111|1|11|1. Понятно, что разным покупкам соответствуют разные комбинации из 7 единиц (в нашем случае мы покупаем 7 пирожных) и трех палочек (разделители видов). Мы получаем столько единиц, сколько предметов надо купить, т.е. число k, а число палочек будет на 1 меньше, чем число видов предметов, т.е. n-1.
Таким образом, мы получаем перестановки с повторениями из k единиц и n-1 разделителей. Различным наборам соответствуют различные перестановки с повторениями (мы же переставляем единицы в зависимости от покупок), а у каждой перестановки есть своя комбинация. Итак, получаем, что число сочетаний с повторениями из элементов n видов по k равно числу:

| Сочетание с повторениями – это сочетание n объектов по k в предположении, что каждый объект может участвовать в сочетании несколько раз. |
Число сочетаний с повторениями можно вычислить по следующей формуле:

Задача: Сколько различных подарочных наборов из 12 конфет можно составить, если в наличии имеются конфеты трех видов (конфет каждого вида больше 12)?
Решение: Порядок в наборах не имеет значения, поэтому используем формулу сочетаний с повторениями из k=12 элементов, выбираем n=3 вида:

Итак, мы рассмотрели тему сочетания, а также задачи по этой теме. Теперь задания по теме не должны вызывать затруднений, а баллы не пропадут.
Тест по теме “Сочетания с повторениями и без”
Разбор:
Набранные баллы:
5
Смотреть разбор
Отправить тест на проверку?
Ты решил еще не все задания












