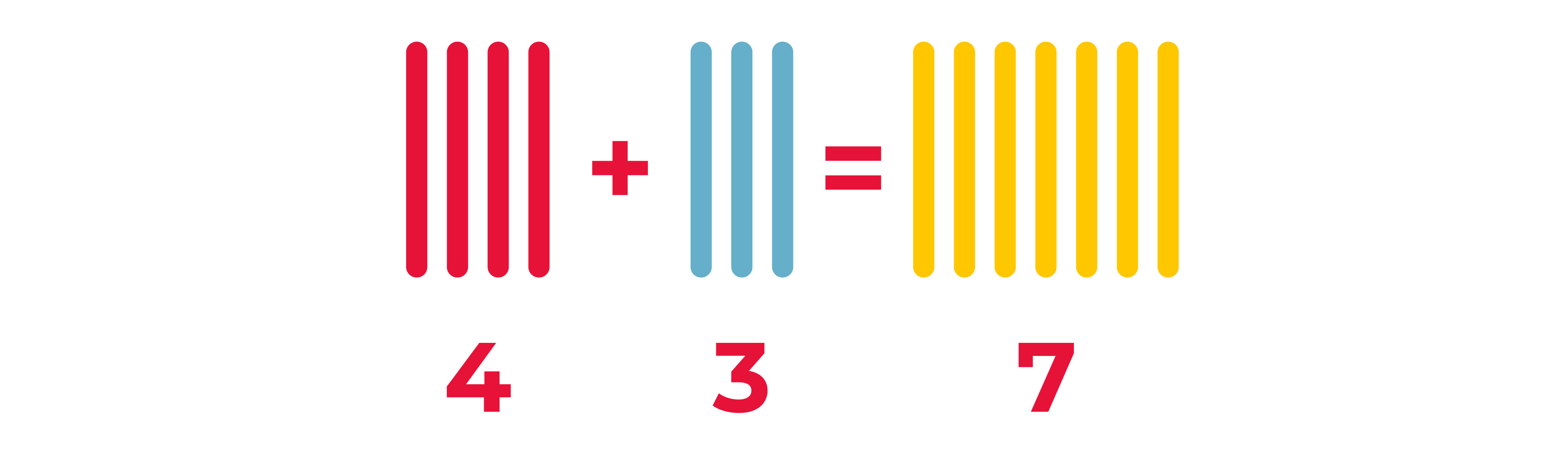Тема, которая напрямую используется в задании 14 и косвенно встречается практически в каждом задании на программирование. Основа информатики и кодирования, так давай же разберемся, что это такое.
| Cистема счисления – это набор символов, необходимых для записи чисел. |
Например, в привычной нам десятичной системе счисления существует 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 для записи различных чисел, а в двоичной на это отводится всего 2 возможных цифры – 0 и 1. Однако этого уже достаточно, чтобы записать любое число.
Чисто теоретически любое число можно записать, используя всего одну цифру, такой системой вы пользовались в детском саду, когда выкладывали палочки на стол в количестве равном нужному числу. Так, каждая палочка обозначала единицу, а итоговое число было суммой всех выложенных.
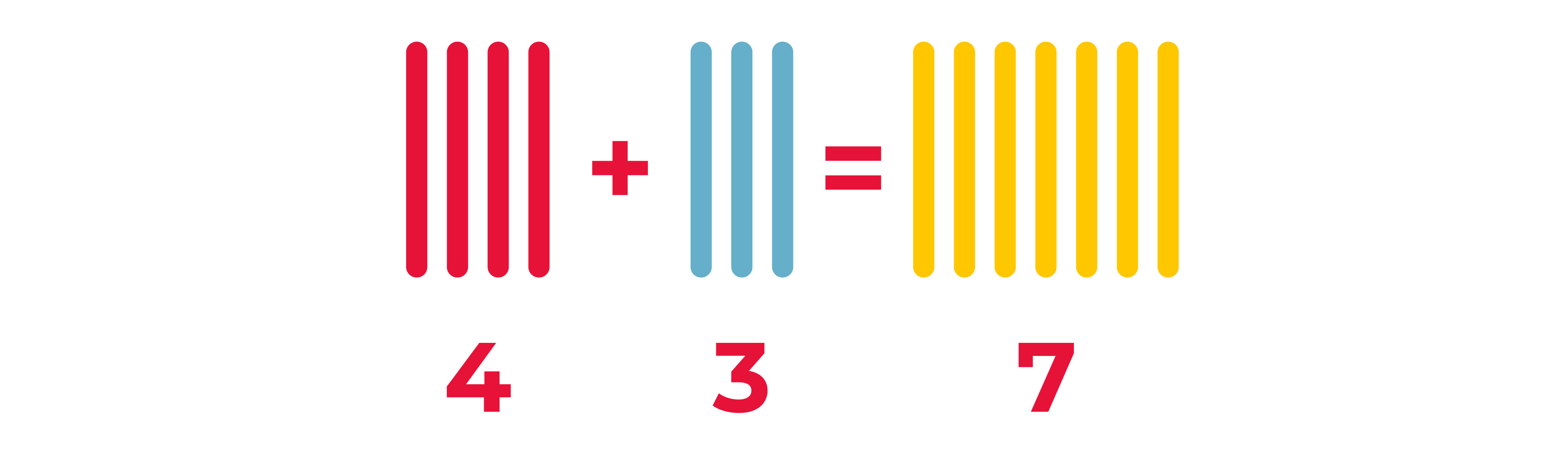

Непозиционная и позиционная системы счисления
- Кстати, такая система счисления называется непозиционной, потому что позиция палочки в числе никак не влияет на ее значение, она всегда останется равной 1.
Еще один популярной непозиционной системой является римская: I – это всегда 1, где бы в числе она не стояла, X – это всегда 10.
Примечание: очевидно, что позиция цифры в римском числе влияет на конечное число, ведь если цифра стоит справа, то ее необходимо прибавить, а если слева – вычесть, но прошу обратить внимание, что мы говорим именно о самой цифре. Значение цифры всегда одинаково, независимо от того, вычитаем мы ее или складываем.
- Арабская же система счисления, привычная нам, является позиционной – позиция цифры в числе влияет на ее значение. Например, в числе 21: первая двойка – это 20, а в числе 42: двойка – это 2.

Почему 10-ричная система счисления работает именно так?
Но притормозим. Для начала разберемся, почему же привычная нам 10-ричная работает именно так. Мы уже выяснили, что в 10-ричной системе счисления существует 10 цифр: от 0 до 9, которыми мы можем обозначать наши числа. Значит для первых 10 чисел, можно смело использовать наши цифры, но что будет когда они у нас закончатся?
Почему же число 10 выглядит именно как единица и ноль?
На самом деле все просто. Мы ведь потратили все цифры, чтобы обозначить числа от 0 до 9, а значит, для того, чтобы обозначить число десять, нам нужна какая-то новая комбинация: все однозначные комбинации заняты, поэтому нам придется использовать двузначные. Ноль на первом месте стоять не может, значит ставим туда 1, а вторая цифра пойдет по порядку, и самая первая – это 0. Вот и получаем число 10.
Далее меняем вторую цифры по возрастанию, пока не используем все до числа 19. В этой ситуации уже необходимо менять первую цифру на большую и подставлять к ней все возможные: получим числа от 20 до 29. И по аналогии так до 99. Когда двузначные комбинации заняты, мы добавляем еще одну цифру и получаем 100, и далее по понятному алгоритму…

Хорошо, схема понятна, но чем же тогда отличается 2-ичная система счисления?
Ответ прост – двоичная система счисления – это десятичная, из которой убрали цифры с 2 до 9. Она содержит всего два возможных символа 0 и 1, поэтому для обозначения чисел 0 и 1 мы можем использовать их, а вот для числа 2 у нас уже нет свободных цифр, поэтому мы вынуждены переходить к двузначным кодам:
| 10-тичная СС |
2-ичная СС |
| 2 |
10 |
| 3 |
11 |
Теперь у нас и двузначные тоже закончились, значит составляем трехзначные:
| 10-тичная СС |
2-ичная СС |
| 4 |
100 |
| 5 |
101 |
| 6 |
110 |
| 7 |
111 |
И эта схема работает в абсолютно любой p-ричной системе счисления. Количество цифр в p-ричной системе счисления равно p. Это все цифры начиная с 0 до p-1.
Однако если в системе счисления, основание которых меньше десятичной, мы забираем какие-то цифры, то в системах, где основание больше 10, появляются новые цифры? Ответ: да. Наверняка вы уже встречались с 16-ричной системой счисления. И давайте разберемся подробнее:
Раз система 16-ричная, значит в ней можно использовать все цифры от 0 до 15, но подождите: 15 это ведь не цифра, как и 10. Для того, чтобы не путать двузначные числа и двузначные цифры придумали обозначать их буквами:
| 10-тичная СС |
16-ричная СС |
| 10 |
A |
| 11 |
B |
| 12 |
C |
| 13 |
D |
| 14 |
E |
| 15 |
F |
Если в 10-ичной СС у вас существует всего 10 цифр, то в 16-ричной – их целых 16. Представьте, что у вас 16 пальцев, и вы без проблем можете сосчитать от 0 до 15.
А вот теперь, когда все возможные цифры от 0 до F этой системы счисления исчерпаны, мы вынуждены составлять двузначные комбинации:
| 10-тичная СС |
16-ричная СС |
| 16 |
10 |
| 17 |
11 |
| ... |
... |
| 31 |
1F |
| 32 |
20 |
Все это объясняет, каким образом работают системы счисления, и как тесно они связаны с темой комбинаторики.
Тест по теме “Позиционные и непозиционные системы счисления”
Разбор:
Набранные баллы:
5
Смотреть разбор
Отправить тест на проверку?
Ты решил еще не все задания