В других статьях мы уже рассмотрели базовые правила суммы и произведения. А теперь переходим к более сложным темам. Первое, что мы рассмотрим, – это перестановки.

Всевозможные перестановки некой совокупности объектов мы можем получить, выставляя их по очереди в ряд в любом порядке. Разные порядки предметов в ряду и будут являться перестановками.

Допустим на столе лежат 3 предмета: ручка, ластик, карандаш. Выкладываем их слева направо в следующем порядке:

ручка / ластик / карандаш

Одна комбинация уже записана выше, и с остальными проблем не возникает:

ручка / карандаш / ластик 
ластик / ручка / карандаш
ластик / карандаш / ручка
карандаш / ручка / ластик
карандаш / ластик / ручка

Итого: 6 комбинаций или 6 перестановок.

Пфф…Легко, понятно даже первокласснику.

Сколько можно составить четырехбуквенных «слов» из букв слова «ДЫНЯ»?

Разумеется под «словами» подразумеваются просто различные комбинации букв, им необязательно быть осмысленными. Эту задачку можно легко решить, используя правило произведения, которое мы рассмотрели в предыдущей статье. Для удобства можно изобразить 4 позиции, на которых мы будем расставлять наши буквы.

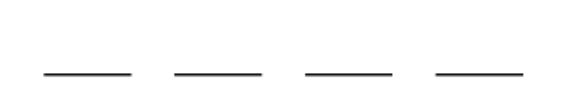
На первое место мы можем поставить любую из четырех букв, на третье место остается любая буква, кроме первой. Аналогично на третье место остается 2 буквы и 1 на последнее:

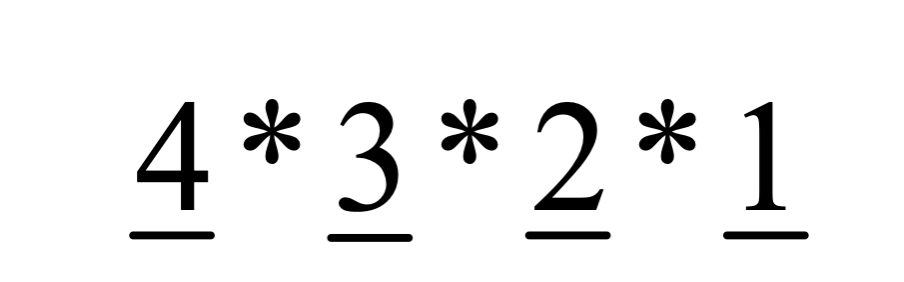
Таким образом, получаем, что количество перестановок равно: 

Полное дерево всех комбинаций, которые нам бы пришлось расписать, выглядит вот так:

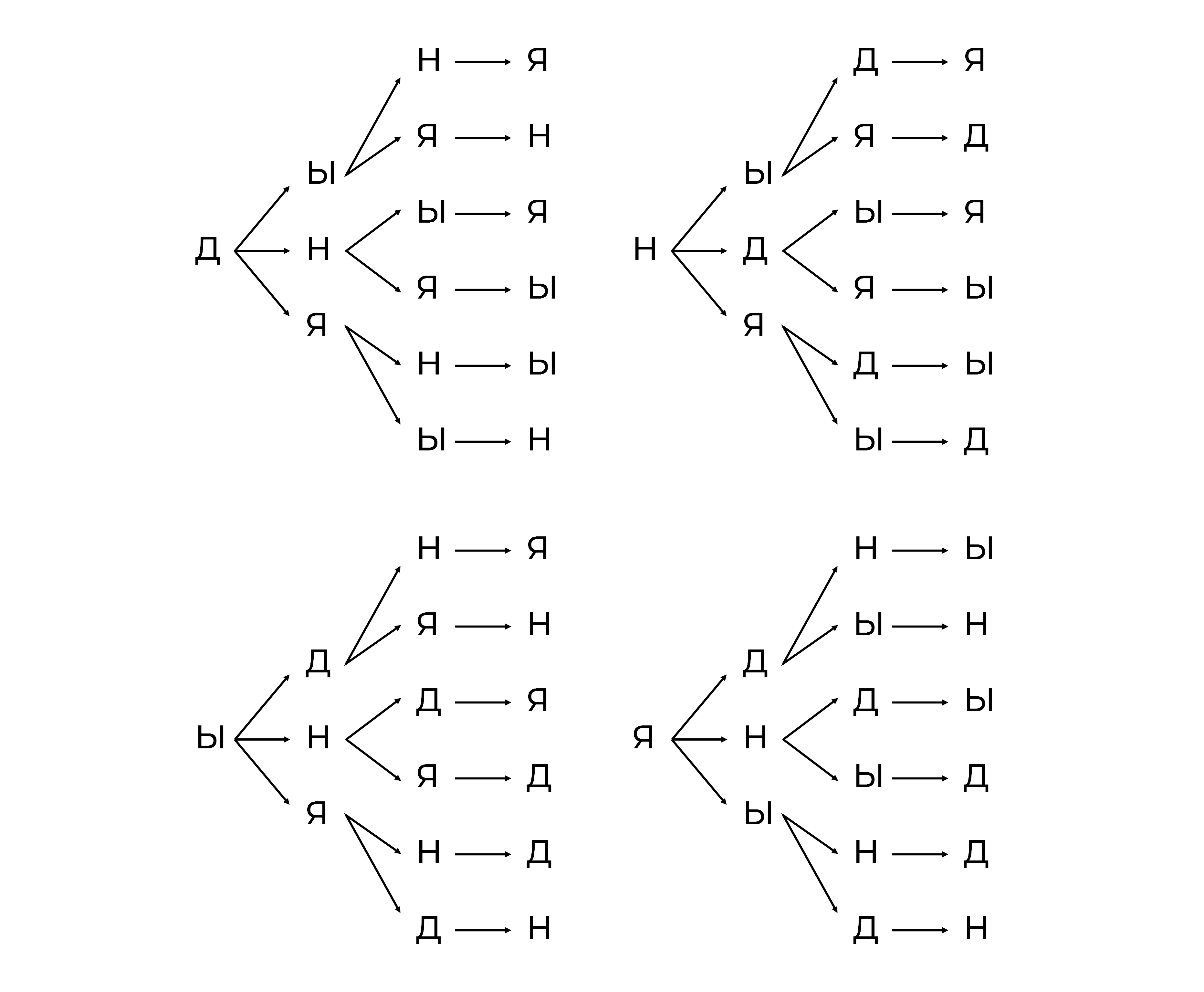
Теперь, зная формулу можем дать определение:

Их число вычисляется по выведенной нами формуле:

Символ n! называется факториалом и обозначает произведение всех целых чисел от 1 до n. По определению, считают, что 0!=1, 1!=1. По сути, перестановка без повторений есть частный случай размещения без повторений, при котором объем выборки равен мощности исходного множества.

Количество перестановок без повторений из n элементов определяется следующей формулой:

Эту формулу, кстати, легко получить, если учесть, что . Тогда получим:

Вроде бы все очевидно, но не спешите с выводами… 

Допустим, что в уже известной нам задаче про канцелярские принадлежности у нас также имеются: ручка, ластик и при этом 2 одинаковых карандаша. Выкладываем их слева направо в следующем порядке:

ручка / ластик / карандаш / карандаш

Вопрос первый: сколькими способами их можно переставить?

Казалось бы, ответ очевиден: у нас 4 предмета, значит, ответ – факториал четырех, но ответ не верный.

Дело в том, что, меняя между собой одинаковые карандаши, наша последовательность меняться не будет!

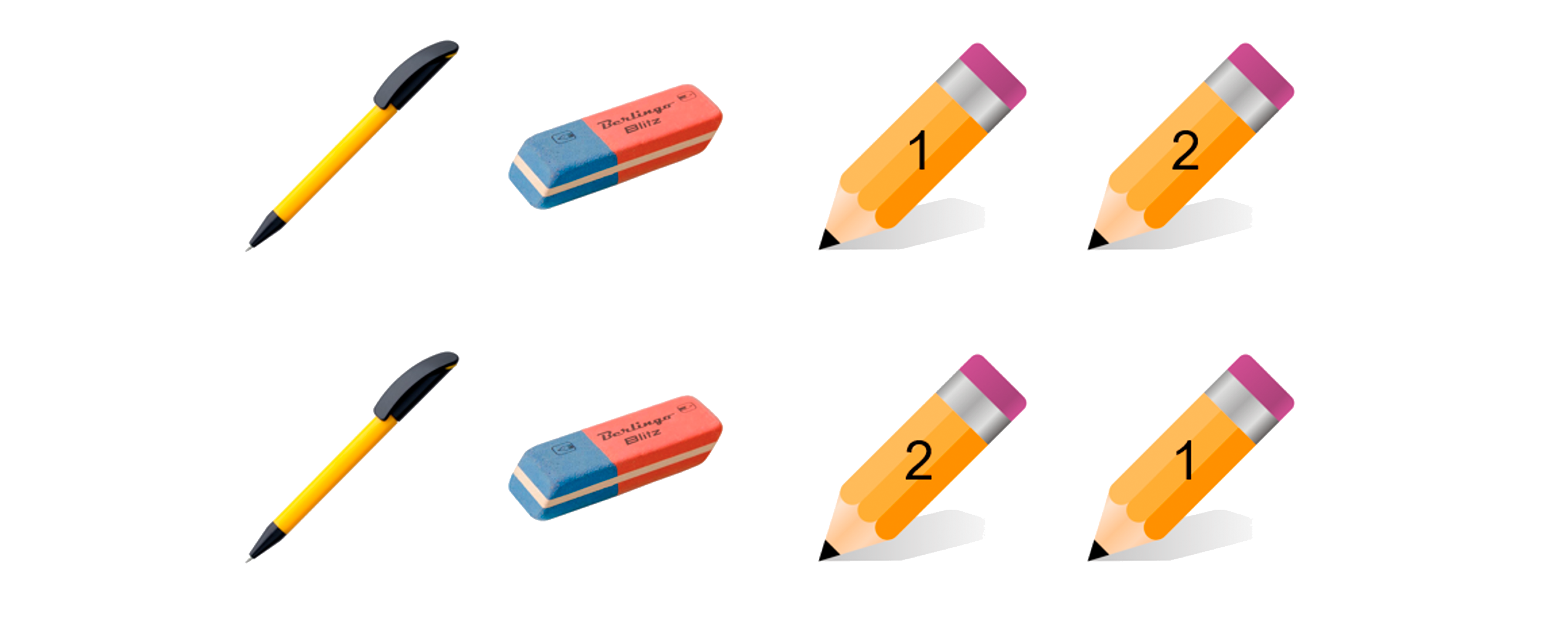
Поэтому полное число перестановок нужно поделить на количество перестановок этих двух одинаковых карандашей.

Всего перестановок четырех предметов: 4!= 24
перестановки двух карандашей: 2!= 2

Итого: 24/2 = 12 комбинаций.

Общее количество перестановок с повторениями определяется формулой:

Задача: Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?

Решение:

В слове: 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно полному числу перестановок 9 букв, деленному на отдельные перестановки четырех букв И и 3 букв С:

Итак, в этой статье мы разобрали тему перестановки и способы решения различных задач. Теперь вы точно получите важные баллы. Успехов!