Если мы говорим о системах счисления, то нужно понимать, что это не только переводы. Число остается числом в любой записи, поэтому их также можно складывать, вычитать, умножать, что может потребоваться в ЕГЭ.

Давайте начнем с понимания того, как работает привычная нам 10-ичная система счисления. В других системах все будет проходить по аналогии и тем же самым правилам.
Сложение
Мы уже знаем, что в десятичной системе есть цифры только от 0 до 9, соответственно, если при сложении получается число большее 9, то мы вынуждены перенести единицу (десяток) в следующий разряд. Например, при сложении 9 + 9 мы получаем 18: единица уходит в следующий разряд, а восьмерку мы оставляем.
Все то же самое работает и в системах счисления с другим основанием. Единственное отличие – это число, при котором происходит переполнение и необходимость переноса. По сути оно является основанием системы счисления. Как ты понимаешь, в двоичной системе – 2. У нас существуют только цифры 0 и 1, поэтому 1+1 в двоичной системе будет выглядеть как 102.
Как несложно сообразить данное правило будет работать для всех систем счисления. Как только мы получаем число большее основания, мы переносим 1 в следующий разряд.
Давай разберемся на примерах:

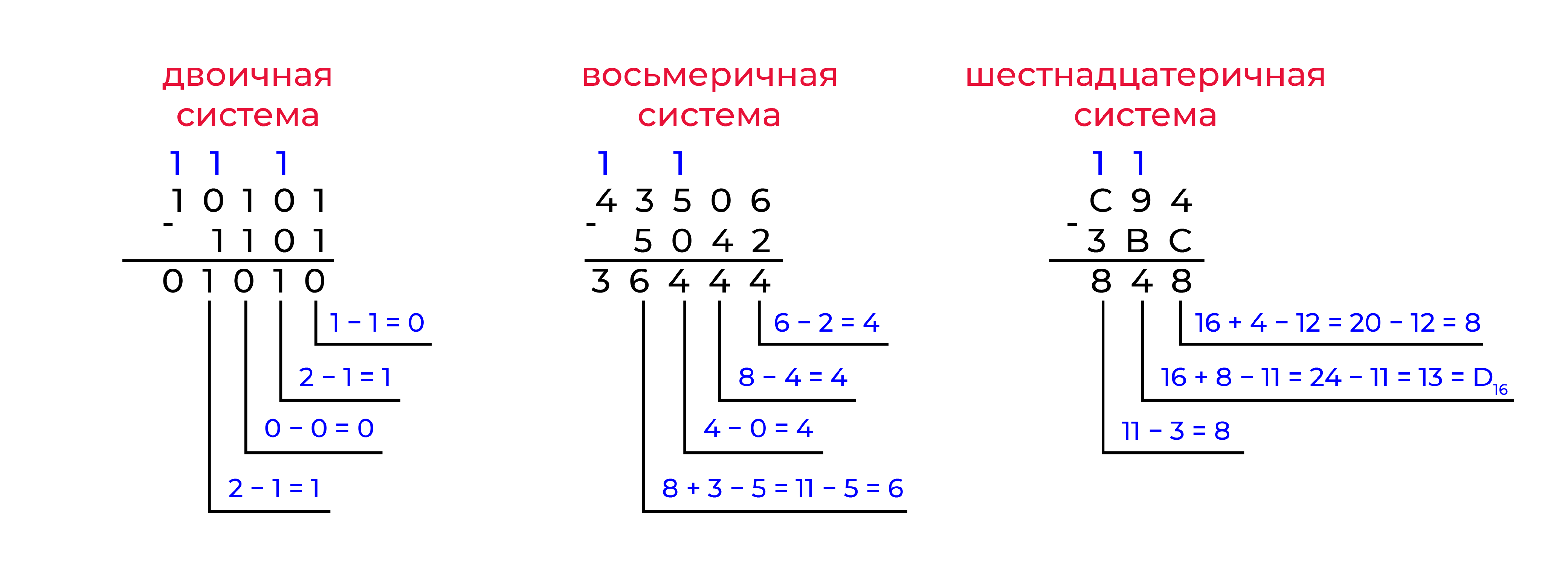
Вычитание
В десятичной системе счисления мы занимали десяток, тут же мы будем занимать то число, которое является основанием этой системы счисления.
Умножение и деление
- Умножение столбиком тоже можно выполнить без особых усилий, главное помнить по переполнение: если в результате умножения получается число большее основания системы счисления, то нужно перенести количество вхождений основания системы счисления в полученное число, а остаток записать в результат.
Например, при умножении 5 на 6 в восьмеричной системе мы получим 30, но в эти 30 восьмерка входит 3 раза, и остается 30 - 3*8 = 6, значит получится 368.
Убедимся на примерах:
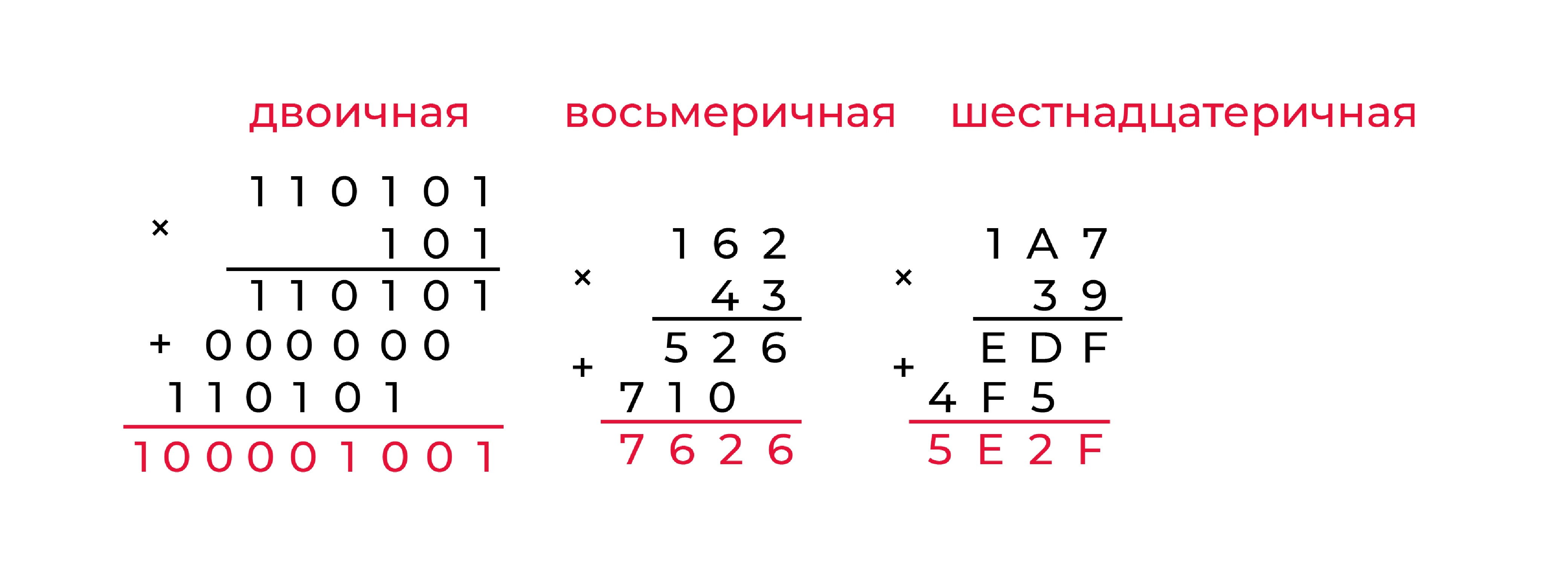
Как видно все работает как и в 10-ичной системе счисления.
- Те же самые действия мы самое мы выполняем и с делением. Однако в качестве примеров я буду рассматривать числа, которые делятся друг на друга без остатков, дабы не затрагивать тему «дополнительный код» и «представление дробных чисел», речь о которых пойдет в следующих статьях.

Итак, мы разобрали тему арифметические операции в разных СС. Она поможет вам в решении заданий на экзамене. Успехов!
Тест по теме “Арифметические операции чисел в разных системах счисления”
Разбор:
Набранные баллы:
5
Смотреть разбор
Отправить тест на проверку?
Ты решил еще не все задания