Алгоритм Дейкстры

Начнем с того, что:

Важное уточнение: он работает только для графов без рёбер отрицательного веса, но в ЕГЭ таковые и не встречаются.

• Представь, что у нас есть вот такой граф, и нам необходимо найти кратчайшее расстояние от вершины 1 до всех остальных.

• Первое, что нам предстоит сделать – пометить вершину 1 меткой ноль, а все остальные – бесконечностью. Дело в том, что пока что мы не знаем расстояние до вершин и обозначаем их каким-то очень большим числом, впоследствии, если мы найдем путь короче, то уже обновим эту метку. Ну, а вершина 1 помечается нулем, потому что от вершины 1 до самой себя расстояние 0.

• Начинаем с вершины 1, ее соседями являются вершины 2, 3 и 6. Длина ребра 1-6 равна 14, что меньше бесконечности, поэтому я обновляю бесконечность на 14. Далее длина ребра 1-3 равна 9, что тоже меньше бесконечности, поэтому обновляю метку у вершины 3 на 9. Аналогично метка у вершины 2 обновляется на 7.

• Вершина 1 рассмотрена, мы ее вычеркиваем и проделываем тоже самое со следующей вершиной, с наименьшей меткой – в нашем случае это вершина 2. Ее соседи –  вершины 1, 3 и 4, но вершину 1 мы уже рассмотрели, поэтому анализируем только 3 и 4. Для метки 3 длина пути будет равна расстоянию до метки 2 и длине ребра 2-3, получается 7 + 10 = 17, что больше, чем 9, поэтому эту метку мы обновлять не будем, этот маршрут невыгоден. Для вершины 4 расстояние составит 7+15 = 22, что меньше бесконечности, поэтому обновляем метку.

• Алгоритм, думаю, уже понятен. Следующая не посещенная вершина – 3. Вершины 1 и 2 уже рассмотрены, анализируем только 6 и 4. До вершины 4 расстояние составит 9 + 11 = 20, что меньше 22 обновляем метку на 20. До вершины 6 расстояние составит 9 + 2 = 11, что тоже меньше 14, значит обновляем метку на 11. 

• Остается рассмотреть всего 2 вершины. Берем вершину 6, длина пути до 5 составит 11 + 9 = 20, что меньше бесконечности, поэтому обновляем метку.

• Ну, а через вершину 4 длина пути до 5 составит: 20 + 6 = 26, что больше имеющихся 20, поэтому метку не трогаем. Вершины кончились, а значит алгоритм завершил свою работу. А те метки, которые остались над вершинами, это кратчайшие расстояния от вершины 1 до этой вершины.

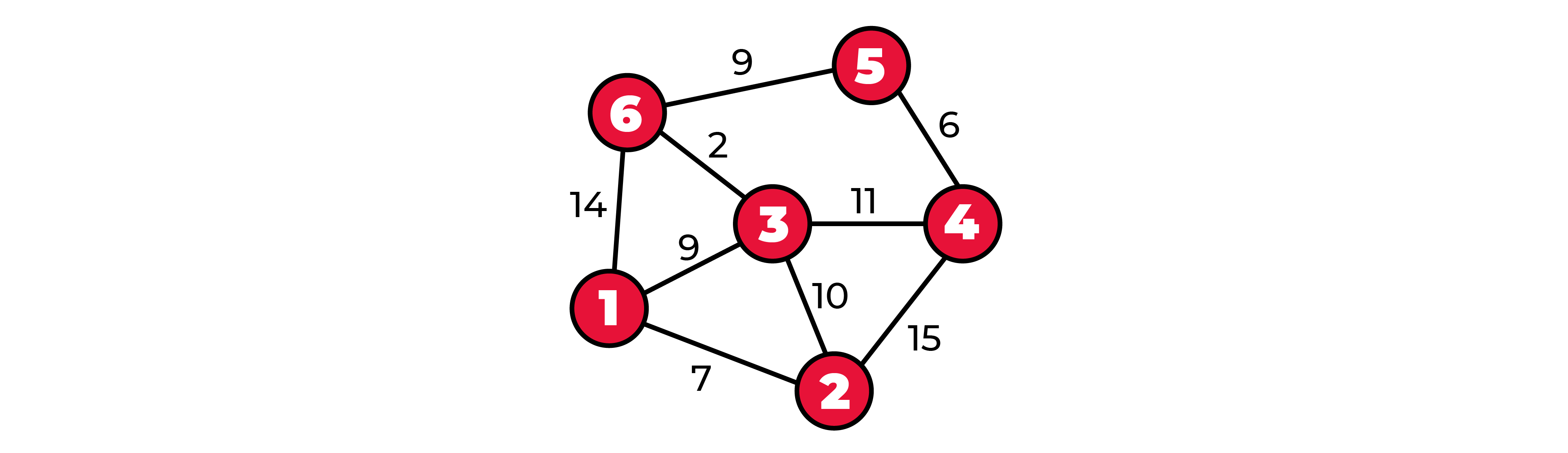
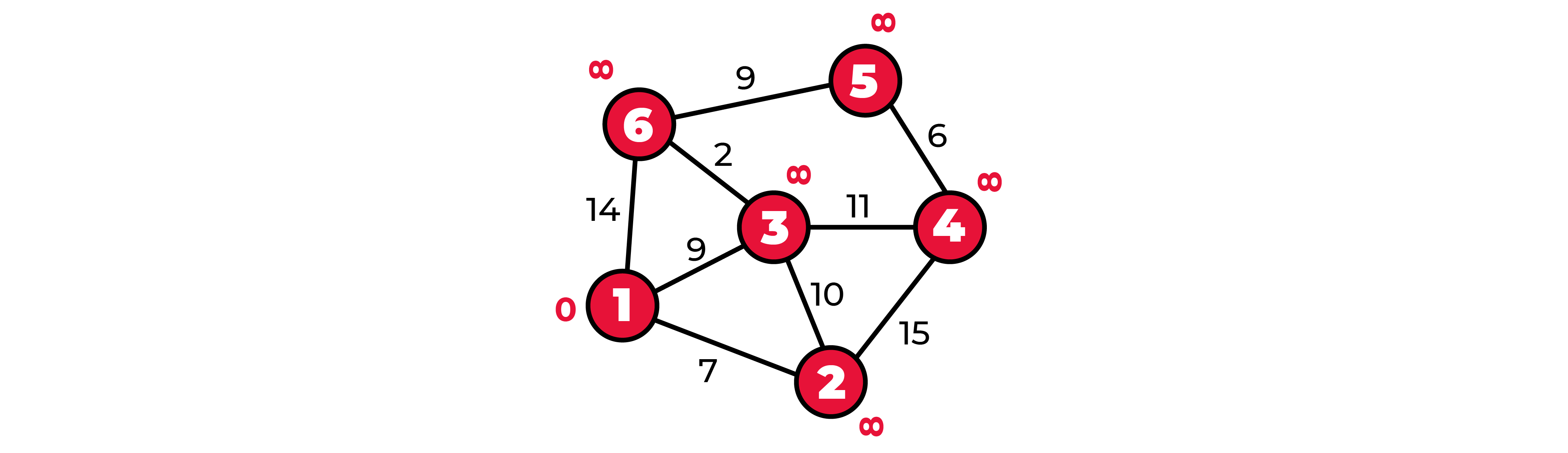
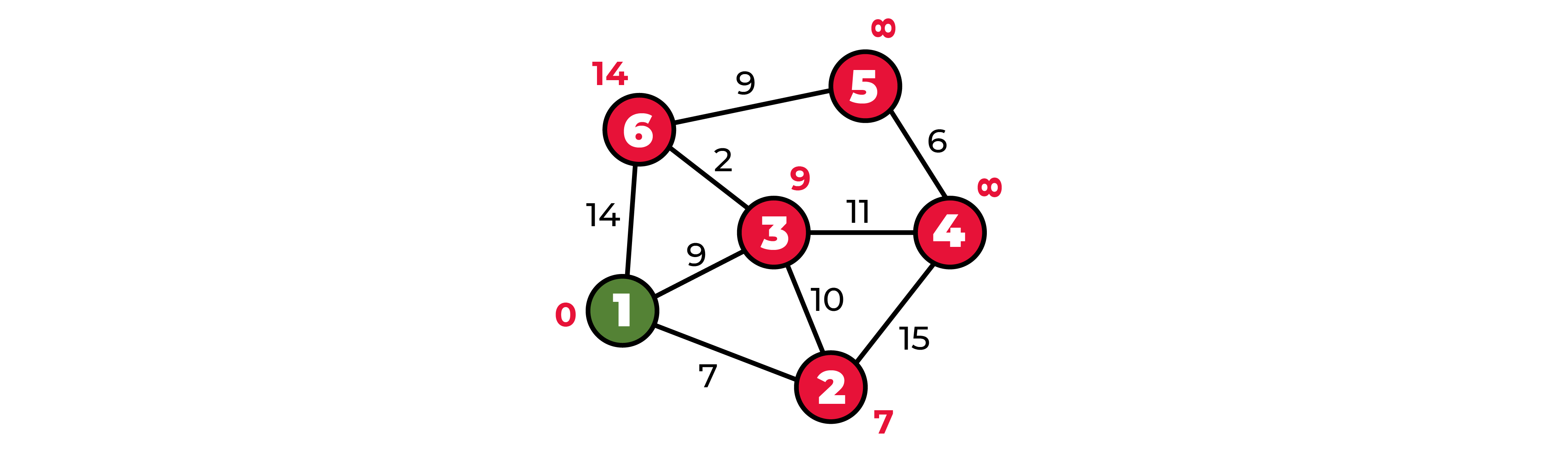
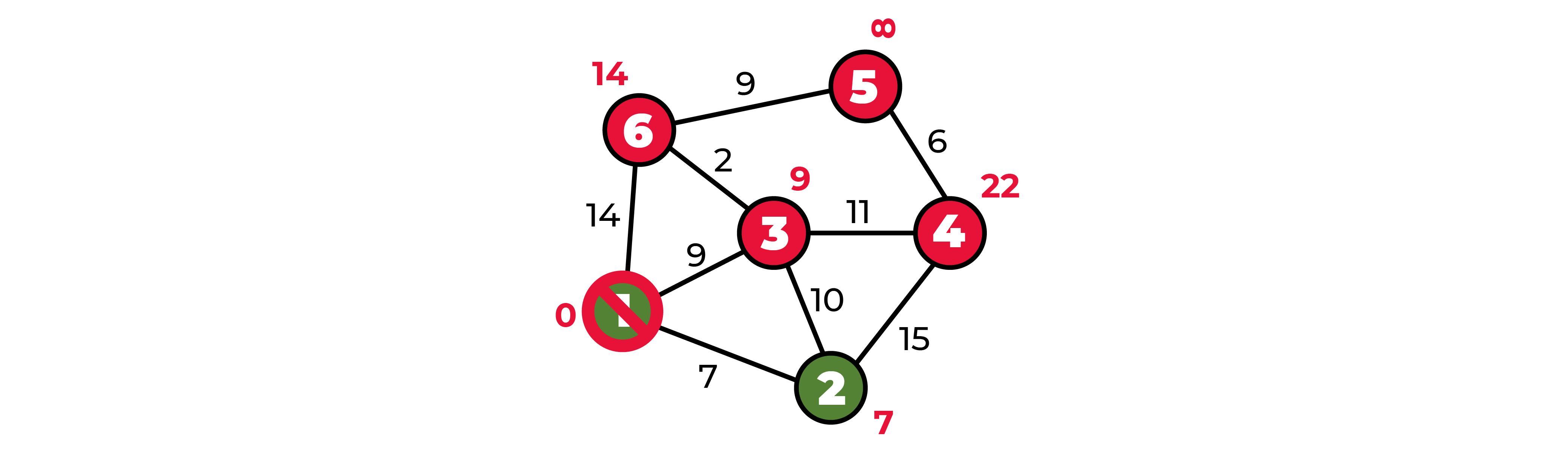
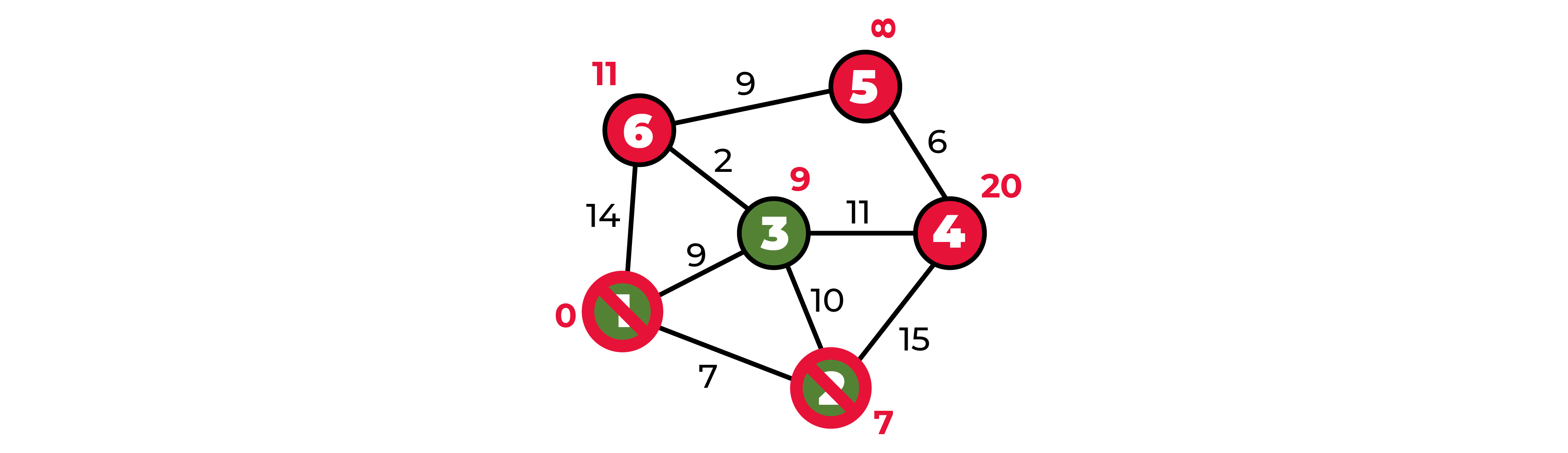
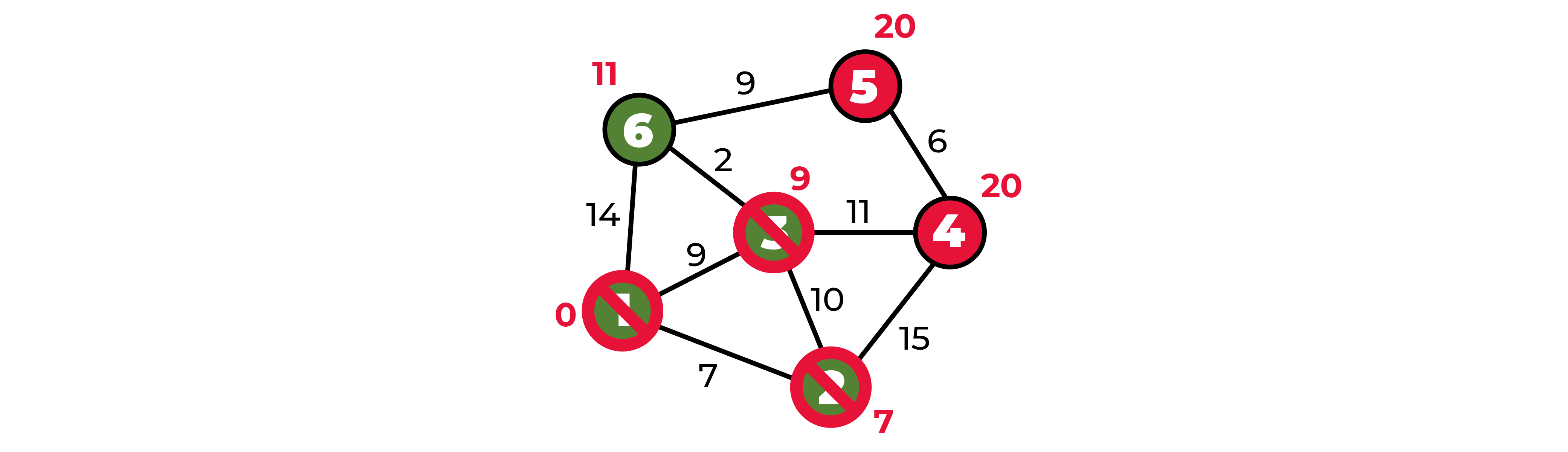
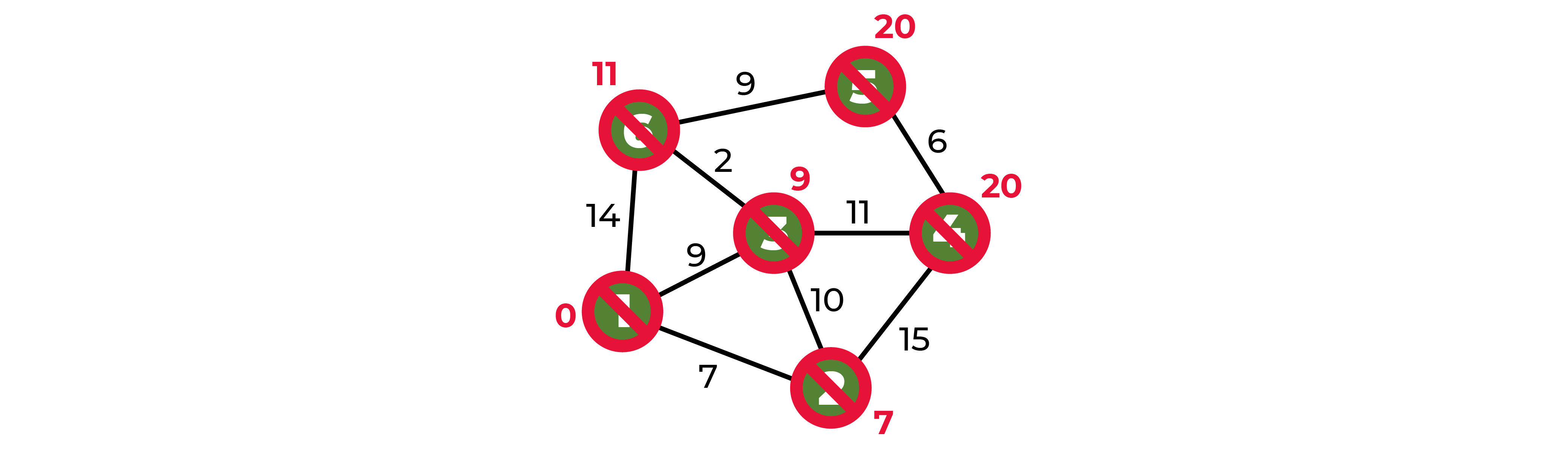
То есть из пункта 1 до пункта 6 можно добраться за 11, до пункта 4 можно добраться за 20.

Теперь с помощью этого алгоритма ты сможешь без труда решать задачи номер 1 и 13, в которых от тебя будут требовать найти кратчайшее расстояние.