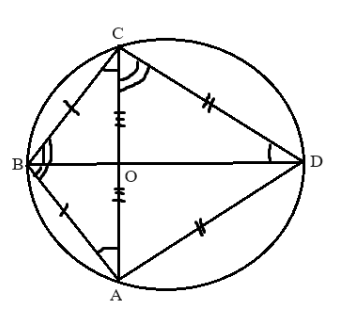
Задача по теме: "Окружности и треугольники"
В четырёхугольнике противоположные стороны не параллельны. Диагонали
четырёхугольника пересекаются в точке О под прямым углом и образуют
четыре подобных треугольника, у каждого из которых одна из вершин - точка О.
a) Докажите, что около четырёхугольника можно описать окружность.
б) Найдите радиус вписанной окружности, если .

Решение:
а)
Все 4 треугольника прямоугольные и подобны => у всех острые углы ,
Внутренние накрест лежащие углы при противоположных сторонах и диагоналях не равны, так как противоположные стороны не параллельны => если угол
или наоборот.
Пусть угол (так как внутр накрест леж при
и сек
); угол
.
-
Если угол
- равнобедренные
можно вписать окружность
-
Если угол
=> - равнобедренные =>
и
можно вписать окр
б) вписанный => диагональ, на которую опираются прямые углы
является диаметром описанной окружности => BD - диаметр, тогда
Решим квадратное уравнение с помощью дискриминанта:
Пусть , тогда:
Ответ:
Сообщение об ошибке
Расскажите, в каком месте допущена ошибка, мы как можно быстрее её исправим. Спасибо за обратную связь!

| МГ | Pro | ProMax | |
| Практика на платформе | |||
| Отслеживание прогресса обучения | |||
| Двухуровневое домашнее задание после каждого вебинара | |||
| Все материалы составлены экспертом ЕГЭ | |||
| Персональный менеджер | |||
| Личный куратор | |||
| Разбор ошибок личным куратором | |||
| Еженедельные созвоны с куратором для закрытия индивидуальных пробелов | |||
| Составление индивидуального расписания |

счёта
средств
подтверждено!
Теперь вы можете приступить
к следующему уроку
курса по математике
замены
Для смены номера телефона
мы отправили Вам код по СМС,
введите его в поле ниже.
Электронная почта
На почту придет чек об оплатеНажимая кнопку "купить", Вы выражаете своё согласие с офертой оказания услуг и принимаете их условия
Здравствуйте!
Выберите информацию о себе ниже

Оплата прошла успешно!