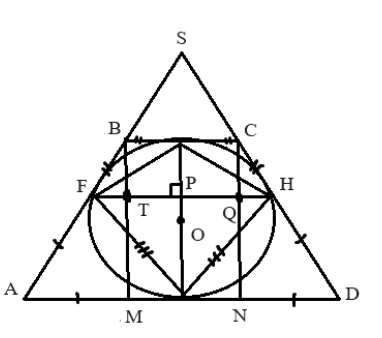
Задача по теме: "Окружности и треугольники"
Около окружности с центром описана трапеция
с основаниями
.
a) Докажите, что треугольник АОВ прямоугольный.
б) Найдите отношение большего основания трапеции к меньшему, если известно, что а площадь четырёхугольника с вершинами в точках касания окружности со сторонами трапеции составляет
площади трапеции
.

Решение:
а)
Перед нами стоит задача доказать одно из свойств вписанной трапеции. Сделать это не сложно:
Если мы продолжим стороны до пересечения точки
, то получим два треугольника:
1) Треугольник , для которого окружность является вписанной - ее центр лежит на пересечении биссектрис углов. То есть
- биссектрисы углов
.
2) Треугольник , для которого окружность является вневписанной - ее центр лежит на биссектрисах внешних углов треугольника, то есть
биссектрисы углов
Углы А и В в сумме равны
градусов (как и углы
).
Биссектрисы разделили эти углы пополам. Значит, сумма «отрезков» углов, то есть градусов. Тогда и углы
равны
градусов, и мы получаем, что треугольник
(также как и
) прямоугольный, что и требовалось доказать.
б) Так как трапеция равнобедренная, точки касания образуют равнобедренные треугольники причем,
- перпендикуляр к
- перпендикуляр к
.
Значит, - высота трапеции, FH параллельно основаниям трапеции.
Введем обозначения частей сторон:
Запишем формулу площади трапеции:
А площадь четырехугольника запишем через перпендикулярные диагонали:
Тогда отношение площадей будет выглядеть так:
успешно сократилось. Теперь нужно подобраться к
. Опустим высоты
. При пересечении с прямой
получим точки
Тогда
складывается из отрезков
причем,
FT можно выразить из подобия треугольников
Найдем
Подставим в формулу отношения площадей:
Теперь составим систему уравнений:
Решаем ее и получаем:
Находим отношения оснований трапеции:
Ответ:
Сообщение об ошибке
Расскажите, в каком месте допущена ошибка, мы как можно быстрее её исправим. Спасибо за обратную связь!

| МГ | Pro | ProMax | |
| Практика на платформе | |||
| Отслеживание прогресса обучения | |||
| Двухуровневое домашнее задание после каждого вебинара | |||
| Все материалы составлены экспертом ЕГЭ | |||
| Персональный менеджер | |||
| Личный куратор | |||
| Разбор ошибок личным куратором | |||
| Еженедельные созвоны с куратором для закрытия индивидуальных пробелов | |||
| Составление индивидуального расписания |

счёта
средств
подтверждено!
Теперь вы можете приступить
к следующему уроку
курса по математике
замены
Для смены номера телефона
мы отправили Вам код по СМС,
введите его в поле ниже.
Электронная почта
На почту придет чек об оплатеНажимая кнопку "купить", Вы выражаете своё согласие с офертой оказания услуг и принимаете их условия
Здравствуйте!
Выберите информацию о себе ниже

Оплата прошла успешно!