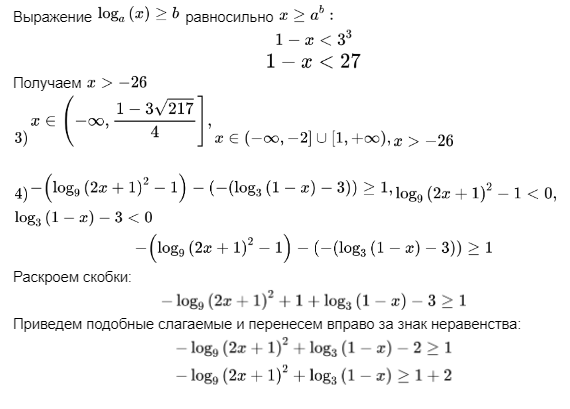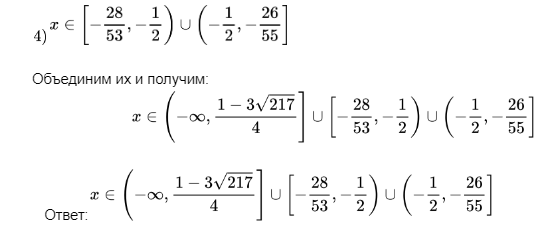Задача по теме: "Смешанные неравенства"
Решите неравенство

Решение:
Определим ОДЗ:
Найдем все значения x,, при которых аргументы логарифма положительны. Решим систему неравенств:
и
Получаем:
и
Объединим эти промежутки:
Вернемся к неравенству и разделим его на четыре возможных случая:
1)
2)
3)
4)
Разберем каждый случай:
1)
Приведем логарифмы к основанию 3:
Преобразуем выражение используя свойства и
Приведем подобные слагаемые, раскрыв скобки:
Перенесем константы вправо за знак неравенства:
Упростим выражение, используя
Выражение равносильно
Так как в выражении есть модуль, то нужно рассмотреть все возможные случаи:
1)
2)
Решим эти неравенства:
1)
Найдем ОДЗ:
Перенесем все слагаемые влево за знак неравенства:
Сообщение об ошибке
Расскажите, в каком месте допущена ошибка, мы как можно быстрее её исправим. Спасибо за обратную связь!

| МГ | Pro | ProMax | |
| Практика на платформе | |||
| Отслеживание прогресса обучения | |||
| Двухуровневое домашнее задание после каждого вебинара | |||
| Все материалы составлены экспертом ЕГЭ | |||
| Персональный менеджер | |||
| Личный куратор | |||
| Разбор ошибок личным куратором | |||
| Еженедельные созвоны с куратором для закрытия индивидуальных пробелов | |||
| Составление индивидуального расписания |

счёта
средств
подтверждено!
Теперь вы можете приступить
к следующему уроку
курса по математике
замены
Для смены номера телефона
мы отправили Вам код по СМС,
введите его в поле ниже.
Электронная почта
На почту придет чек об оплатеНажимая кнопку "купить", Вы выражаете своё согласие с офертой оказания услуг и принимаете их условия
Здравствуйте!
Выберите информацию о себе ниже

Оплата прошла успешно!