Задача по теме: "Гиперболы"
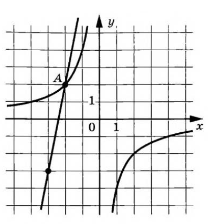
На рисунке изображены графики функций и
которые пересекаются в точках A и B. Найдите абсциссу точки B.
Решение:
– гипербола, не смещенная. Она проходит через точку
подставим ее координаты:
Итого
Найдем уравнение прямой, которая проходит через точку и
Вычтем из второго первое: отсюда
Итого
Найдем в каких точках пересекаются прямая и гипербола:
Домножим уравнение на чтобы избавиться от дробей:
Перенесем все слагаемые влево, чтобы привести квадратное уравнение к каноническому виду:
Для решения воспользуемся формулой дискриминанта и корней квадратного уравнения (корни уравнения можно найти другим способом – по теореме Виета).
Получаем, что является абсциссой точки A, а
– абсцисса точки B.
Ответ: -0,4
Сообщение об ошибке
Расскажите, в каком месте допущена ошибка, мы как можно быстрее её исправим. Спасибо за обратную связь!

| МГ | Pro | ProMax | |
| Практика на платформе | |||
| Отслеживание прогресса обучения | |||
| Двухуровневое домашнее задание после каждого вебинара | |||
| Все материалы составлены экспертом ЕГЭ | |||
| Персональный менеджер | |||
| Личный куратор | |||
| Разбор ошибок личным куратором | |||
| Еженедельные созвоны с куратором для закрытия индивидуальных пробелов | |||
| Составление индивидуального расписания |

счёта
средств
подтверждено!
Теперь вы можете приступить
к следующему уроку
курса по математике
замены
Для смены номера телефона
мы отправили Вам код по СМС,
введите его в поле ниже.
Электронная почта
На почту придет чек об оплатеНажимая кнопку "купить", Вы выражаете своё согласие с офертой оказания услуг и принимаете их условия
Здравствуйте!
Выберите информацию о себе ниже
Электронная почта
На почту придет чек об оплатеНажимая кнопку "купить", Вы выражаете своё согласие с офертой оказания услуг и принимаете их условия

Оплата прошла успешно!