Задача по теме: "Описанные окружности"
Радиус окружности равен Найдите величину тупого вписанного угла, опирающегося на хорду, равную
Ответ дайте в градусах.

Решение:
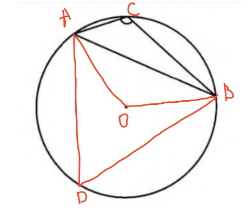
Обозначим центр окружности точкой На хорде
построим центральный угол
и вписанный угол
Известно, что сумма противоположных углов четырехугольника вписанного в окружность равна . Поэтому определив угол
мы сможем вычислить искомый угол.
Вычислим центральный угол Это можно сделать используя теорему косинусов:
Подставим известные величины:
Приведем подобные слагаемые:
Можем избавиться от коэффициента перед косинусом, разделив обе части на
Исходя из этого угол значит дуга
содержащая точку
равна
Из этого следует, что величина дуги которая не содержит точку
равна
Вписанный угол равен половине величины дуги, на которую опирается:
Ответ: 120
Сообщение об ошибке
Расскажите, в каком месте допущена ошибка, мы как можно быстрее её исправим. Спасибо за обратную связь!

| МГ | Pro | ProMax | |
| Практика на платформе | |||
| Отслеживание прогресса обучения | |||
| Двухуровневое домашнее задание после каждого вебинара | |||
| Все материалы составлены экспертом ЕГЭ | |||
| Персональный менеджер | |||
| Личный куратор | |||
| Разбор ошибок личным куратором | |||
| Еженедельные созвоны с куратором для закрытия индивидуальных пробелов | |||
| Составление индивидуального расписания |

счёта
средств
подтверждено!
Теперь вы можете приступить
к следующему уроку
курса по математике
замены
Для смены номера телефона
мы отправили Вам код по СМС,
введите его в поле ниже.
Электронная почта
На почту придет чек об оплатеНажимая кнопку "купить", Вы выражаете своё согласие с офертой оказания услуг и принимаете их условия
Здравствуйте!
Выберите информацию о себе ниже

Оплата прошла успешно!